Q2.8 Assume n continuous random variables fX1, X2, , Xng jointly follow a multivariate Gaussian distribution Nx j , . a. For any random variable

Q2.8 Assume n continuous random variables fX1, X2, , Xng jointly follow a multivariate Gaussian distribution N¹x j , º.

a. For any random variable Xi (8i), derive its marginal distribution p¹Xiº.

b. For any two random variables Xi and Xj (8i, j), derive the conditional distribution p¹Xi jXj º.

c. For any subset of these random variables S, derive the marginal distribution for S.

d. Split all n random variables into two disjoint subsets S1 and S2, and then derive the conditional distribution p¹S1 jS2º.

Hints: Some identities for the inversion and determinant of a symmetric block matrix, where 11 2 Rpp,

12 2 Rpq, 22 2 Rqq, are as follows:

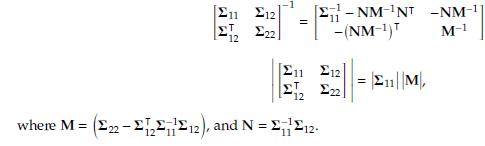
1 212 = 22 12 1 12 T -NM-NT -NM-11 -(NM-1)T , 22 12 where M= (22-12), and N = 212- M-1 =211||M,