Q4.3 Deriving the PCA under the minimum error formulation (II): Given a set of N vectors in an n-dimensional space: D =

x1, x2, , xN

(xi 2 Rn), we search for a complete orthonormal set of basis vectors

wj 2 Rn j j = 1, 2, , n

, satisfying w|j wj0 =

1 j = j0 0 j , j0 . We know that each data point xi in D can be represented by this set of basis vectors as xi =

Ín j=1 ¹w|j xiºwj . Our goal is to approximate xi using a representation involving only m

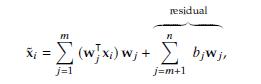
where fbj j j = m + 1, , ng in the residual represents the common biases for all data points in D. If we minimize the total distortion error

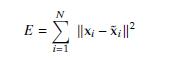
with respect to both
w1,w2, ,wm
and fbj g:

a. Show that the m optimal basis vectors
wj
lead to the same matrix A in PCA.

b. Show that using the optimal biases fbj g in Eq. (4.4) leads to a new reconstruction formula converting the m-dimensional PCA projection y = Ax to the original x, as follows:
˜x = A|y +
????
I ????A|A
¯x, where ¯x = 1 N ÍN i=1 xi denotes the mean of all training samples in D.

residual m X = = (wx) + j=1 n j=m+1 bjWj,