a. Express 1.4 sin 5.6 cos in the form R sin ( ), where R and are constants, R >

a. Express 1.4 sin θ − 5.6 cos θ in the form R sin (θ − α), where R and α are constants, R > 0 and 0 < α < 90°. Round R and α to 3 decimal places.

b. Hence find the maximum value of 1.4 sin θ − 5.6 cos θ and the smallest positive value of θ for which this maximum occurs.

The length of daylight, d(t) at a location in northern Scotland can be modelled using the equation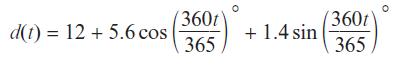

where t is the numbers of days into the year.

c. Calculate the minimum number of daylight hours in northern Scotland as given by this model.

d. Find the value of t when this minimum number of daylight hours occurs.

d(t) = 12 + 5.6 cos 360t 365 + 1.4 sin 360t 365