g(x) = e x 1 + 2x 15 a. Show that the equation g(x) =
Question:
g(x) = ex − 1 + 2x − 15
a. Show that the equation g(x) = 0 can be written as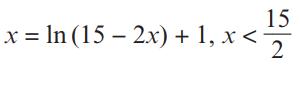
The root of g(x) = 0 is α. The iterative formula xn + 1 = ln (15 − 2xn) + 1, x0 = 3, is used to find a value for α.
b. Calculate the values of x1, x2 and x3 to 4 decimal places.
c. By choosing a suitable interval, show that α = 3.16 correct to 2 decimal places.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
a ex1 2x 15 0 e1 15 2x b c x1 ln 15 2x x ...View the full answer
Answered By
Rustia Melrod
I am a retired teacher with 6 years of experience teaching various science subjects to high school students and undergraduate students. This background enables me to be able to help tutor students who are struggling with the science of business component of their education. Teaching difficult subjects has definitely taught me patience. There is no greater joy for me than to patiently guide a student to the correct answer. When a student has that "aha!" moment, all my efforts are worth it.
The Common Core standards are a useful yardstick for measuring how well students are doing. My students consistently met or exceeded the Common Core standards for science. I believe in working with each student's individual learning styles to help them understand the material. If students were struggling with a concept, I would figure out a different way to teach or apply that concept. I was voted Teacher of the Year six times in my career. I also won an award for Innovative Teaching Style at the 2011 National Teaching Conference.
4+ Reviews
10+ Question Solved
Related Book For 
Pearson Edexcel A Level Mathematics Pure Mathematics Year 2
ISBN: 9781292183404
1st Edition
Authors: Greg Attwood, Jack Barraclough, Ian Bettison, David Goldberg, Alistair Macpherson, Joe Petran
Question Posted:
