Complete the implementation of the Skip List-based dictionary begun in Section 16.3.1. Section 16.3.1: 16.3.1 Skip Lists

Complete the implementation of the Skip List-based dictionary begun in Section 16.3.1.

Section 16.3.1:

Transcribed Image Text:

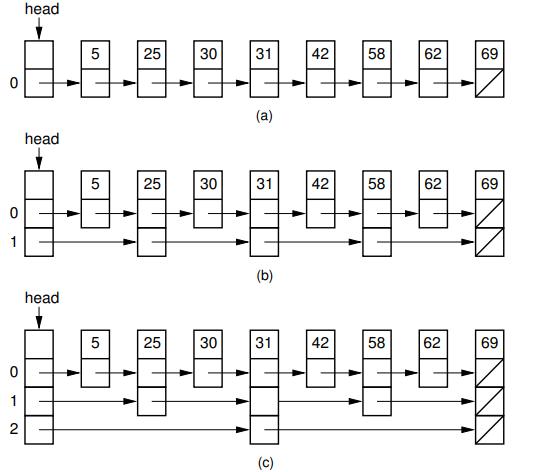
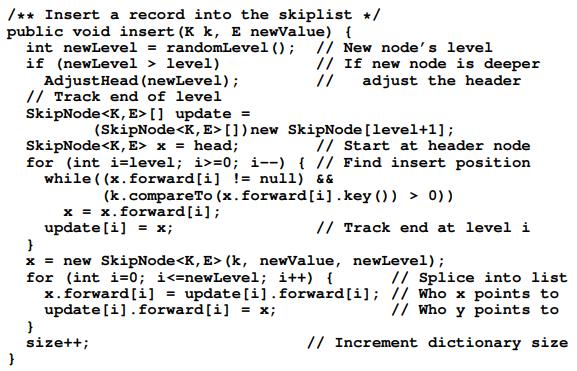
16.3.1 Skip Lists Skip Lists are designed to overcome a basic limitation of array-based and linked lists: Either search or update operations require linear time. The Skip List is an example of a probabilistic data structure, because it makes some of its decisions at random. Skip Lists provide an alternative to the BST and related tree structures. The pri- mary problem with the BST is that it may easily become unbalanced. The 2-3 tree of Chapter 10 is guaranteed to remain balanced regardless of the order in which data values are inserted, but it is rather complicated to implement. Chapter 13 presents the AVL tree and the splay tree, which are also guaranteed to provide good per- formance, but at the cost of added complexity as compared to the BST. The Skip List is easier to implement than known balanced tree structures. The Skip List is not guaranteed to provide good performance (where good performance is defined as (log n) search, insertion, and deletion time), but it will provide good perfor- mance with extremely high probability (unlike the BST which has a good chance of performing poorly). As such it represents a good compromise between difficulty of implementation and performance. Figure 16.2 illustrates the concept behind the Skip List. Figure 16.2(a) shows a simple linked list whose nodes are ordered by key value. To search a sorted linked list requires that we move down the list one node at a time, visiting (n) nodes in the average case. Imagine that we add a pointer to every other node that lets us skip alternating nodes, as shown in Figure 16.2(b). Define nodes with only a single pointer as level 0 Skip List nodes, while nodes with two pointers are level 1 Skip List nodes. To search, follow the level 1 pointers until a value greater than the search key has been found, then revert to a level 0 pointer to travel one more node if necessary. This effectively cuts the work in half. We can continue adding pointers to selected nodes in this way - give a third pointer to every fourth node, give a fourth pointer to every eighth node, and so on- until we reach the ultimate of log n pointers in the first and middle nodes for a list of n nodes as illustrated in Figure 16.2(c). To search, start with the bottom row of pointers, going as far as possible and skipping many nodes at a time. Then, shift up to shorter and shorter steps as required. With this arrangement, the worst-case number of accesses is (log n).