A special class of first-order linear equations have the form a(t)y' (t) + a' (t)y(t) = f(t), where a and fare given functions of t. Notice that the left side of this equation can be written as the derivative of a product, so the equation has the form

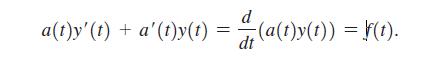
Therefore, the equation can be solved by integrating both sides with respect to t. Use this idea to solve the following initial value problems.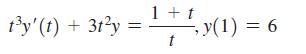

a(t)y' (t) + a'(t)y(t) = (a(t)y(t)) = f(t).