Question: Evaluate the line integral in Stokes Theorem to evaluate the surface integral s ( F) n ds. Assume that n points in

Evaluate the line integral in Stokes’ Theorem to evaluate the surface integral ∫∫_s(∇ × F) • n ds. Assume that n points in the positive z-direction.

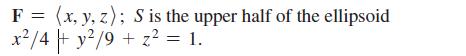
F = (x, y, z); S is the upper half of the

F = (x, y, z); S is the upper half of the ellipsoid x/4 + y/9 + z = 1.

Step by Step Solution

★★★★★

3.35 Rating (164 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To evaluate the line integral in Stokes Theorem and subsequently the surface integral we need to follow these steps Step 1 Determine the boundary curv... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus 1st Questions!

Evaluate the line integral in Stokes Theorem to evaluate the surface integral s ( F) n ds. Assume that n points in the positive z-direction. F = (x + y, y + z, z + x); S is the tilted disk...

Evaluate the line integral in Stokes Theorem to evaluate the surface integral s ( F) n ds. Assume that n points in the positive z-direction. F = (2y, -2, its base) x + y + z xyz); S is the cap of...

find one example from the news media that you can link --either videos, podcasts, articles, reports, television broadcasts, etc.--that exhibit what you take to be a valid and sound deductive argument.

Evaluate the line integral in Stokes' Theorem to evaluate the surface integral (V XF) . n dS. Assume that n points in an upward direction. S F = (x+ y,y+ z,z + x) ; S is the tilted disk enclosed by...

Evaluate the line integral in Stokes' Theorem to evaluate the surface integral S ( g r a d F ) * n d S . Assume that n points in an upward direction. F = ( : x + y , y + z , z + x : ) ; S is the...

" [ 2 0 points ] Evaluate the line integral i n Stokes Theorem t o evaluate the surface integral S F * d S for the following vector field and surface. Assume that the normal vector n points i n a n...

Evaluate the line integral i n Stokes' Theorem t o find the surface integral S ( g r a d F ) * n d S . Assume that n i s i n the positive z - direction. F = ( : x , y , z : ) ; S i s the upper half o...

opts Evaluate the line integral in Stokes' Theorem to find the surface integral (V x F) . ndS, where F(x, y, z) = (4y, -xz, e yz), and S is the part of the JJ s paraboloid z = x2 + y that lies inside...

please help! Evaluate the line integral in Stokes' Theorem to find the value of the surface integral | (V xF) - n ds. Assume that S n points in an upward direction. F= (x.y.z) : S is the upper half...

i need help with this step Evaluate the line integral in Stokes' Theorem to find the value of the surface integral | |(V x F) . n dS. Assume that n points in an upward direction. S F = (x,y,z) ; S is...

Recommendation: Which one of the 3 alternatives discussed for topic 9 do you recommend for the firm? Why do you make that recommendation? What are the risks (think about which stakeholders might be...

The current population of a small city is 29500 people. Due to a loss of jobs, the population is decreasing by an average of 450 people per year. How many years (from now ) will it take for the...

12.10 How do we build in seasonal variation in our forecast?

B. Discuss the importance of knowing which people in an audience are decision makers.

Are Canadian public servants gaming the system by taking more sick days than do private sector workers? To answer the question Statistics Canada took a random sample of white-collar private sector...

Which Canadians give the most to charity? A Statistics Canada study took random samples of men and women and recorded the amount donated to charity in the previous year. Is there sufficient evidence...

Refer to Exercise 13.49. The NCPA conducted another study, this one on alcohol. They randomly sample low-income and middle-income alcohol drinkers and determined how much each spends annually on...

Alliance Corp. issues 2,110 shares of $8 par value common stock at $16 per share. When the transaction is recorded, what credit entry or entries are made? Select the correct answer. Common Stock...

Based on the following information, compute cash flows from financing activities. Purchase of short-term investments Dividends paid Interest paid Additional short-term borrowing from bank $ 620 820...

The following are the typical classifications used in a balance sheet: Required: For each of the following balance sheet items, use the letters above to indicate the appropriate classification...