Question: Verify that the line integral and the surface integral of Stokes Theorem are equal for the following vector fields, surfaces S, and closed curves C.

Verify that the line integral and the surface integral of Stokes’ Theorem are equal for the following vector fields, surfaces S, and closed curves C. Assume that C has counterclockwise orientation and S has a consistent orientation.


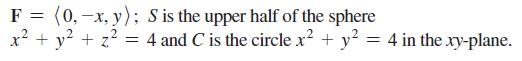
F = (0, -x, y); x + y + z2: = S

F = (0, -x, y); x + y + z2: = S is the upper half of the sphere 4 and C is the circle x + y = 4 in the xy-plane.

Step by Step Solution

★★★★★

3.51 Rating (151 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

To verify the equality of the line integral and surface integral of Stokes Theorem for the given vector field surface and closed curve well follow the ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Precalculus 1st Questions!

Q:

Verify that the line integral and the surface integral of Stokes Theorem are equal for the following vector fields, surfaces S, and closed curves C. Assume that C has counterclockwise orientation and...

Q:

Verify that the line integral and the surface integral of Stokes Theorem are equal for the following vector fields, surfaces S, and closed curves C. Assume that C has counterclockwise orientation and...

Q:

Verify that the line integral and the surface integral of Stokes Theorem are equal for the following vector fields, surfaces S, and closed curves C. Assume that C has counterclockwise orientation and...

Q:

I need it asap Verify that the line integral and the surface integral of Stokes' Theorem are equal for the following vector field, surface S, and closed curve C. Assume that C has counterclockwise...

Q:

Verify that the line integral and the surface integral of Stokes Theorem are equal for the following vector fields, surfaces S, and closed curves C. Assume that C has counterclockwise orientation and...

Q:

Verify that the line integral and the surface integral of Stokes Theorem are equal for the following vector fields, surfaces S, and closed curves C. Assume that C has counterclockwise orientation and...

Q:

Verify that the line integral and the surface integral of Stokes' Theorem are equal for the following vector field, surface S, and closed curve C. Assume that C has counterclockwise orientation and S...

Q:

Verify that the line integral and the surface integral of Stokes' Theorem are equal for the following vector eld. surface S, and closed curve C. Assume that C has counterclockwise orientation and S...

Q:

Please help! Verify that the line integral and the surface integral of Stokes' Theorem are equal for the following vector field, surface S, and closed curve C. Assume that C has counterclockwise...

Q:

Verify that the line integral and the surface integral of Stokes' Theorem are equal for the following vector field, surface S, and closed curve C. Assume that C has counterclockwise orientation and S...

Q:

When developing your answer, be sure to define the relevant concepts and apply them via examples from companies you have researched (from The Wall Street Journal and other business periodicals) or...

Q:

Standard International Ltd. who is a foreign trade creditor having its office in Hong Kong wanted to file a petition under the Insolvency and Bankruptcy Code, 2016 on the default of the debtor in...

Q:

Question 1 0 1 pts The static budget variance is the difference between the and the amounts for the fexible budget; amounts for the static budget fleolble budget varlance: actlility fevel varlance...

Q:

LO14.5 Use the story line approach to presentations.

Q:

A statistics professor was in the process of comparing the pass rates (the percentage of entering students who graduate in 5 years or less) for B.A.s, B.B.A.s, B.Sc.s, and B.Eng.s. Delving into the...

Q:

Refer to Exercise 6.59. In exercise 6.59 Given the following probabilities, compute all joint probabilities. P(A) = .9 P(A c ) = .1 P(B/A) = .4 P(B/A c ) Determine P(A / B).

Q:

Refer to Exercise 6.60. In exercise 6.60 Determine all joint probabilities from the following. P(A) = .8 P(A c ) = .2 P(B\A) = .4 P(B\A c ) = .7 Find the following. a. P(A | B) b. P(A C | B) c. P(A |...

Q:

Dawson Toys, Ltd., produces a toy called the Maze. The company has recently established a standard cost system to help control costs and has established the following standards for the Maze toy:...

Q:

CableVision has been approached by the City of Mirada to run its cable operations in 2019. After negotiating with key parties, CableVision has made the following agreements: It will offer Mirada...

Q:

Required information The following information applies to the questions displayed below. Warnerwoods Company uses a perpetual inventory system. It entered into the following purchases and sales...