a Assume that P(x) and Q(x) are continuous over the interval a, b Use the Fundamental Theorem of Calculus, Part 1, to show that any function y satisfying the equation for (x) e P(x) dx is a solution to the first order linear equation b If then show that any solution y in part (a) satisfies the initial condition y(x 0 ) y 0 v(x)y f VCX v(x)Q(x) dx C

Question: a. Assume that P(x) and Q(x) are continuous over the interval [a, b]. Use the Fundamental Theorem of Calculus, Part 1, to show that any

a. Assume that P(x) and Q(x) are continuous over the interval [a, b]. Use the Fundamental Theorem of Calculus, Part 1, to show that any function y satisfying the equation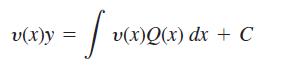 v(x)y = f VCX v(x)Q(x) dx + C

for ν(x) = e^∫^{P(x) dx} is a solution to the first-order linear equation.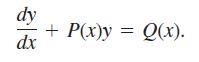

b. If 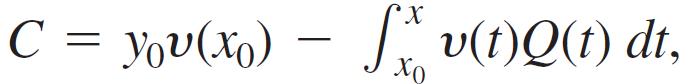then show that any solution y in part (a) satisfies the initial condition y(x₀) = y₀.

v(x)y = f VCX v(x)Q(x) dx + C

Step by Step Solution

★★★★★

3.47 Rating (170 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a To begin we take the derivative of both sides of the given equation with respect to x using the Fu... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Assume the hypotheses of Exercise 3, and assume that y 1 (x) and y 2 (x) are both solutions to the firstorder linear equation satisfying the initial condition y(x 0 ) = y 0 . a. Verify that y(x) = y...

Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function. 8. g(x) = (" In t dt 7. g(x) = VT+ 21 dt sin t dt dx 10. glu) = 9. g(y) 11. F(x) = cos(r) dt Hint: [" costr?)...

In problems, use the Second Fundamental Theorem of Calculus to evaluate each definite integral (a) (b) (c) x3 dx 0 x dx -1 3x22x 3) dx -1

CONCORDIA UNIVERSITY Department of Mathematics & Statistics Course Mathematics Examination Final Instructors: Special Instructions: Number 205 Date April 2016 A. Boyarsky, E. Duma, E. Ghandimi, J....

Please show me the solution for this question #5 Thank you Q5. Find the derivatives of the functions. (a) fox) = px2 Sin(t?) dt Vx (b) g (x) = sinc cos ( J x2+ 1 )). Fundamental Theorem Calculus Part...

please do it fast 2. Thanos claims that the universe has grown too rapidly to sustain itself. He makes his argument mathematically by conjecturing that the universal population at a given time t,...

(6) (Variant of Theorem 7.17) Suppose {f,) is a sequence of functions which are differentiable on [a, b], with each f, continuous on [a, b], and {f,(xo)} converges for some xo E [a, b]. Use the...

PLEASE HELP ME SOLVE THESE QUESTIONS! THANKS! 3. (a) Let k : X C R" - R be a function defined on the finite set X = {X1, X2, ....., In} . Argue that k achieves a minimum and a maximum on X. Is this a...

1. Let f(x) = 1-2\\al (a) Compute the left Riemann sum L; and right Riemann sum Rs for the function f(x) = 1- 2 x| on the interval [=1, 2]. (b) Use the fundamental theorem of calculus to compute the...

Discussion #2 - Process Costing A+ This week we are learning about Process Costing, when similar items are produced in large quantities. For your discussion this week, give me an an example of a...

Dollars Day Printers Cartridges School Supplies 1 19 57 $1,634.00 2 15 60 $945.00 3 15 60 $1,245.00 4 15 75 $840.00 5 16 80 $1,424.00 6 14 42 $1,260.00 7 10 40 $530.00 8 12 36 $972.00 9 20 80...

Whathorse Company has the followincselected trinuactiond during March Mar. PurdNased equiproint costing 5 7 5 3 0 from Bole Compory on account. 2 S Recehwd credt of $ 5 3 0 from Careell Compury for...

In a two-page report, summarize your calculations. Be sure to indicate the date you obtained the information and how your calculations could help managers and employees, investors, lenders, and...

Sketch the curve with the given polar equation by first sketching the graph of r as a function of in Cartesian coordinates. r = 1 - cos

Sketch the curve with the given polar equation by first sketching the graph of r as a function of in Cartesian coordinates. r = 1 + 2 cos

Sketch the curve with the given polar equation by first sketching the graph of r as a function of in Cartesian coordinates. r ?, -2 S 0

A call option matures in six months. The underlying stock price is $64, and the stock's return has a standard deviation of 40 percent per year. The risk-free rate is 8.0 percent per year, compounded...

Marcus is a new, self-employed tax preparer who lives in a small apartment in New York City. He has 120 clients and meets them at their place of business or the local coffee shop. Marcus' apartment...

Cost Accounting A You are asked to bring the following incomplete Gizelle Co, accounts up to date through Mwy 2018. Also consider the additional information in pesos that follows the T-accounts...