Question: (a) Find the polynomial P 1 (x) = a 0 + a 1 x whose value and slope agree with the value and slope of
(a) Find the polynomial P1(x) = a0 + a1x whose value and slope agree with the value and slope of f(x) = cos x at the point x = 0.
(b) Find the polynomial P2(x) = a0 + a1x + a2 x2 whose value and first two derivatives agree with the value and first two derivatives of f(x) = cos x at the point x = 0. This polynomial is called the second-degree Taylor polynomial of f(x) = cos x at x = 0.
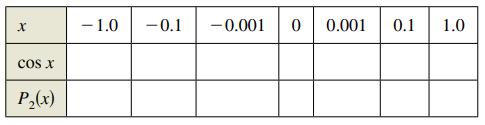
(c) Complete the table comparing the values of f(x) = cos x and P2(x). What do you observe?
(d) Find the third-degree Taylor polynomial of f(x) = sin x at x = 0.
X COS X P(x) -1.0 -0.1 -0.001 0 0.001 0.1 1.0
Step by Step Solution
3.42 Rating (161 Votes )
There are 3 Steps involved in it
ANSWER a Since the value and slope of fx cos x at x 0 are both equal to 1 we can write P1x a0 a1x To ... View full answer

Get step-by-step solutions from verified subject matter experts


