A function (x, y) is homogeneous of degree n (n a nonnegative integer) if (tx, ty) t n (x, y) for all t, x, and y For such a function (sufficiently differentiable), prove that af x a X b x y 2x af dy nf(x, y) (avis) 3 (101) 2xy n(n 1)f

Question: A function (x, y) is homogeneous of degree n (n a nonnegative integer) if (tx, ty) = t n (x, y) for all t, x,

A function ƒ(x, y) is homogeneous of degree n (n a nonnegative integer) if ƒ(tx, ty) = tⁿƒ(x, y) for all t, x, and y. For such a function (sufficiently differentiable), prove that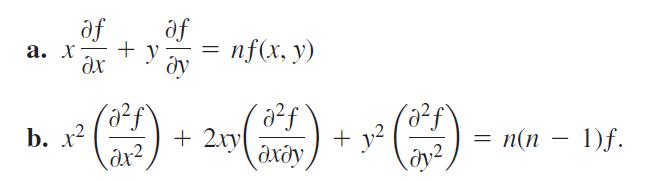 af x a. X- b. x + y 2x af dy =

af x a. X- b. x + y 2x af dy = nf(x, y) (avis) + 3 (101) + 2xy = n(n 1)f.

Step by Step Solution

★★★★★

3.47 Rating (160 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Lets assume that fxy is homogeneous of degree n Then we have ftxty t... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

A function ((X, Y) is homogeneous of degree ( if, when we multiply each argument by a constant , f(X,Y) = (((X, Y). Thus, if a function is homogeneous of degree zero, ((X,Y) = 0( (X, Y) = ((X, Y),...

A function f(x) on Rn is called homogeneous of degree k if f(cx) = ci(x) for all scalars c. (a) If a Rn is a fixed vector, show that a linear form (x) = a . x = a1X1 +-----+ anxn is homogeneous of...

If a differentiable functional f is homogeneous of degree k, its partial derivatives are homogeneous of degree of k - 1.

In Exercises determine whether the function is homogeneous, and if it is, determine its degree. A function (x, y) is homogeneous of degree n if (tx, ty) = t n (x, y). f(x, y) = x + 3xy - 2y

In Exercises determine whether the function is homogeneous, and if it is, determine its degree. A function (x, y) is homogeneous of degree n if (tx, ty) = t n (x, y). f(x, y) xy x + y

In Exercises determine whether the function is homogeneous, and if it is, determine its degree. A function (x, y) is homogeneous of degree n if (tx, ty) = t n (x, y). f(x, y) = x + y

In Exercises determine whether the function is homogeneous, and if it is, determine its degree. A function (x, y) is homogeneous of degree n if (tx, ty) = t n (x, y). X f(x, y) = 2 In- y

In Exercises determine whether the function is homogeneous, and if it is, determine its degree. A function (x, y) is homogeneous of degree n if (tx, ty) = t n (x, y). f(x, y) = tan y X

In Exercises determine whether the function is homogeneous, and if it is, determine its degree. A function (x, y) is homogeneous of degree n if (tx, ty) = t n (x, y). f(x, y) = x 4xy + y

In Exercises determine whether the function is homogeneous, and if it is, determine its degree. A function (x, y) is homogeneous of degree n if (tx, ty) = t n (x, y). f(x, y) = 2 In xy

Treatment of adenosine with nitrous acid gives a nucleoside known as inosine:

Refer to Exhibit 1.1. For a regular corporation, prepare a list of the following: Exhibit 1.1 a. Income items that are taxed (specifically, items included in realized income) b. Items excluded from...

A project has a payback period of one year, a negative NPV and a positive IRR. Is this possible? Group of answer choices No , because a project with a positive IRR has a positive NPV No , because...

=+a. Construct a stem-and-leaf display of the data. Will the sample mean or the sample median be larger for this data set?

In Exercises 2934, evaluate c F dr. F(x, y) = xyi + yj C: r(t) = 4 cos ti + 4 sin tj, 0 t EIN

Consider Sketch an open connected region around the smooth curve C shown in the figure such that you can use Theorem 15.7 to evaluate c F dr. Explain how you created your sketch. F(x, y) = y x + y...

In Exercises 2934, evaluate c F dr. F(x, y) = xi + yj C: r(t) = (3t+1)i + tj, 0 t 1

issued an additional 5000 shares of common stock in exchange for $25000.recorded the cash as sales revenue how can i get the journal entry?

Consider normal costing and actual costing. In bullet point form, Describe each of these systems and discuss the most significant similarities and differences between them. answer wuickly

The following data were taken from the records of Blumbey Manufacturing Company for the fiscal year ended June 30, 2012. Raw Materials Inventory 7/1/11 $48,310 Factory Insurance $4,180 Raw Materials...