A function (x, y, z) is said to be harmonic in a region D in space if it satisfies the Laplace equation throughout D. a.

A function ƒ(x, y, z) is said to be harmonic in a region D in space if it satisfies the Laplace equation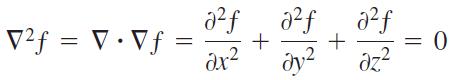

throughout D.

a. Suppose that ƒ is harmonic throughout a bounded region D enclosed by a smooth surface S and that n is the chosen unit normal vector on S. Show that the integral over S of ∇ƒ · n, the derivative of ƒ in the direction of n, is zero.

b. Show that if ƒ is harmonic on D, then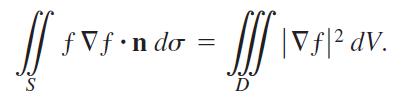

Vf = V.Vf= afafaf + + dx dy dz = 0