Question: (a) Given a circular sector with radius L and central angle (see figure), show that the area of the sector is given by S

(a) Given a circular sector with radius L and central angle θ (see figure), show that the area of the sector is given by S = 1/2 L²θ.

(b) By joining the straight-line edges of the sector in part (a), a right circular cone is formed (see figure) and the lateral surface area of the cone is the same as the area of the sector. Show that the area is S = πrL, where r is the radius of the base of the cone.

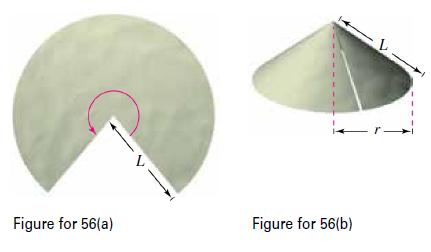
Figure for 56(a) Figure for 56(b)

(c) Use the result of part (b) to verify that the formula for the lateral surface area of the frustum of a cone with slant height L and radii r₁ and r₂ (see figure) is S = π(r₁ + r₂)L.

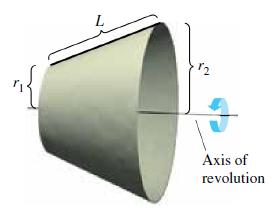
Figure for 56(a) Figure for 56(b)

Step by Step Solution

★★★★★

3.45 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

ANSWER a The area of a sector is given by A 12 r2 where r is the radius and is the central angle in ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

If the surface of a cone of slant height C and base radius r is cut along a lateral edge and laid flat, it becomes the sector of a circle of radius C and central angle Î¸ (see Figure 19)....

Show that the area of the part of the surface of a sphere of radius a between two parallel planes h units apart (h

Historically, in order to maintain quality control over munitions (bullets) produced by an assembly line, the manufacturer would use a ballistic pendulum to determine the muzzle velocity of a gun,...

63 Take Quiz Exit Find the arc length of the arc in bold. Leave your answers in terms of pi. ' Previou Next ' 63 Take Quiz Exit Assignment Started: Mar 8 at 8:52pm Quiz Instructions Question 5 1 pts...

circle and other related terms 1.It is the region bounded by two radii and their intercepted arc. A. Sector of a circle C. central angle B. Segment of a circle D. intercepted angle 2. To get the area...

Hope you can help me. What's More Try to answer more challenging set of problems and activities about the area of the sectors and segments and problems involving tangents and secant segments. A. Use...

PRINTABLE VERSION Practice Final Question 1 Suppose that is an acute angle of a right triangle and that sec() = a) csc() = 33 7 b) csc() = 7 33 33 c) 33 4 csc() = 33 d) csc() = 33 4 e) csc() = 7 33...

Must answer all questions in 30 min! Answer with confident correct answers ( Double check to see if the answers are correct!) I need the answers ASAP! Question number 9. A car has wheels with a 4...

Need help with this multi-part question on derivatives. Please fill out the 3 charts. Variable r is the radius and variable P is the perimeter. I'll give helpful rating :) Advancing Oil Slick Because...

4. [-/1 Points] DETAILS LARPCALC10 4.1.006. Fill in the blank. The area A of a sector of a circle with radius r and central angle 0, where 0 is measured in radians, is given by the formula OA = 10 2...

Davis Steel Distributors is planning to set up an additional warehouse in its distribution network. Analysis of item-sales data for its other warehouses shows that 25 percent of the items represent...

For the function f, use composition of functions to show that f -1 is as given. a. f (x) = 6x - 5, f -1(x) = (x + 5) / 6 b. f (x) = (x + 1) / x, f -1(x) = 1/(x - 1)

Which of the following measures of poverty are debated and discussed ( according to Rank, 2 0 2 1 ) ? Income measure vs . assets measure Absolute measure vs . relative measure Pre - transfer measure...

Obtain the estimates of treatment effects in the design of Exercise 10.9 and use LSD method to compare the treatment effects at 1% level of significance.

In Exercises use Theorem 9.11 to determine the convergence or divergence of the p-series. Data from in Theorem 9.11 THEOREM 9.11 Convergence of p-Series The p-series n=1 1 1 1 = + + nP 1P 2P 1 3P + 1...

In Exercises use the polynomial test given in Exercise 32 to determine whether the series converges or diverges. Data from in Exercise 32 Prove that, if P(n) and Q(n) are polynomials of degree j and...

Please answer carefully. That old equipment for producing oil drums is worn out, said Bill Seebach, president of Hondrich Company. We need to make a decision quickly. The company is trying to decide...

Triple Company's accountant made an entry that included the following items: debit postage expense $12.42; debit office supplies expense $27.33, credit to cash over/short $2.19. If the original...

Equipment was purchased for $150,000. Freight charges amounted to $7,000 and there was a cost of $20,000 for building a foundation and installing the equipment. It is estimated that the equipment...