Question: (a) Let f'(x) be continuous. Show that (b) Explain the result of part (a) graphically. lim h0 f(x+h)-f(xh) 2h = f'(x).

(a) Let f'(x) be continuous. Show that


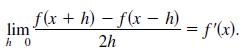
lim h0 f(x+h)-f(xh) 2h = f'(x).


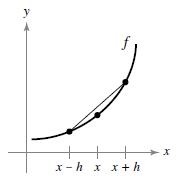
(b) Explain the result of part (a) graphically.


image

lim h0 f(x+h)-f(xh) 2h = f'(x).

Step by Step Solution

★★★★★

3.40 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a Using the definition of the derivative we have fx limh0 fxh fxh Multiplying the numerator ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Q:

Thoroughly explain opportunities and challenges in technology, ethics, social responsibility, organizational culture, and globalization that sport managers face today and in the near future.

Q:

Let A B R, let f : B R and let g be the restriction of f to A (that is, g(x) = f(x) for x A). (a) If f is continuous at c A, show that g is continuous at c. (b) Show by example that if g is...

Q:

Assume that f has an inverse on its domain. a. Let y = f -1 (x) and show that

Q:

1. From the graph of f, state each xvalue at which f is discontinuous. Explain why the function is discontinuous at that point. For each x-value, determine whetherf is continuous from the left, from...

Q:

please help solve step by step odule DDA 40 Be sure to show and explain all work. 10 p Part 1 - Exploration Let f (x) = - 30 1+ 2 3 - x a. Use tables and graphs to find lim f(x) and lim f(x) x 7 0o x...

Q:

PreCalgulus Module 8 DBA 4 in Be sure to show and explain all work. 10 points each Part 1 - Exploration 30 Let f (x) W a. Use tables and graphs to nd lim f (x) and lim for) x > on x -) on b. Identify...

Q:

MA3310 Project Project Topic List Topic: Numerical differentiation Topics and skills: Derivatives, calculator While the rules of differentiation allow us to compute the derivative of just about any...

Q:

Math 104A Homework #2 Instructor: Lihui Chai General Instructions: Please write your homework papers neatly. You need to turn in both full printouts of your codes and the appropriate runs you made....

Q:

Least Squares Approximation Hector D. Ceniceros 1 Least Squares Approximation Let f be a continuous function on [a, b]. We would like to find the best approximation to f by a polynomial of degree at...

Q:

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

Q:

For problem find x, y, or b without a calculator. logb e-2 = -2

Q:

Air with following properties enter the compressor of an aircraft gas turbine P=5.45 Psia T=430 deg R V=600 FPS M=150 lbm/s what is the cross sectional area (ft2)at the inlet ? a) 2.7 b) 1.64 c) 3.27...

Q:

ABC Company uses a periodic inventory system. Here is the information for the year Ended December 31, 2020: Operations Number of units Unit cost Opening stock, January 1, 2020 500 3,25 Purchase...

Q:

Under the CFP Boards Rules of Conduct, which of the following are a category of rules within the CFP Boards Rules of Conduct? a. Obligations to prospective clients and clients. b. Obligations to...

Q:

In Exercises use the disk method or the shell method to find the volumes of the solids generated by revolving the region bounded by the graphs of the equations about the given line(s). (a) The x-axis...

Q:

In Exercises use the disk method or the shell method to find the volumes of the solids generated by revolving the region bounded by the graphs of the equations about the given line(s). revolved about...

Q:

In Exercises use the disk method or the shell method to find the volumes of the solids generated by revolving the region bounded by the graphs of the equations about the given line(s). revolved about...

Q:

Wendell's Donut Shoppe is investigating the purchase of a new $47,300 donut-making machine. The new machine would permit the company to reduce the amount of part-time help needed, at a cost savings...

Q:

25. Geen yln sonunda, Helen's, Inc.'in (yalnzca yl sonunda alnan fiziksel envanter saymyla periyodik bir envanter sistemi kullanr) envanteri 115.000$'a mal olan mallar vard. Cari yln Ocak aynda,...

Q:

Question 3. Theory Questions A. Differentiate between Functional based Costing and Activity based costing B. What are the weaknesses of Functional based costing? C. Give two examples of unit level...