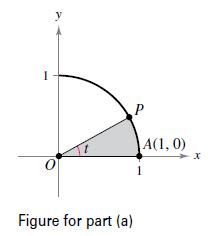
Question: (a) Let P(cos t, sin t) be a point on the unit circle x 2 + y 2 =1 in the first quadrant (see figure).
(a) Let P(cos t, sin t) be a point on the unit circle x2 + y2 =1 in the first quadrant (see figure). Show that t is equal to twice the area of the shaded circular sector AOP.
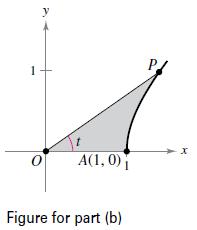
(b) Let P(cosh t, sinh t) be a point on the unit hyperbola x2 - y2 = 1 in the first quadrant (see figure). Show that t is equal to twice the area of the shaded region AOP. Begin by showing that the area of the shaded region AOP is given by the formula
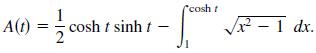
1 y 0 Figure for part (a) P A(1, 0)
Step by Step Solution
3.29 Rating (155 Votes )
There are 3 Steps involved in it
Since the function Gx y z x2 is an even function with res... View full answer

Get step-by-step solutions from verified subject matter experts


