Question: a. Let (x) be a function satisfying |(x)| x 2 for -1 x 1. Show that is differentiable at x =

a. Let ƒ(x) be a function satisfying |ƒ(x)| ≤ x2 for -1 ≤ x ≤ 1. Show that ƒ is differentiable at x = 0 and find ƒ′(0).


b. Show that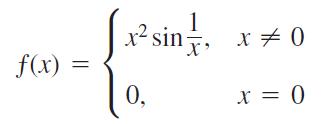f(x) = [x sin 1. 0, x = 0 x = 0


is differentiable at x = 0 and find ƒ′(0).

f(x) = [x sin 1. 0, x = 0 x = 0

Step by Step Solution

★★★★★

3.35 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a To show that is differentiable at x0 we need to sho... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Q:

Use the result of Exercise 21 to show that the following functions are differentiable at x = 0. Data from in Exercise 21 Suppose that the functions and g are defined throughout an open interval...

Q:

Suppose that the functions and g are defined throughout an open interval containing the point x 0 , that is differentiable at x 0 , that (x 0 ) = 0, and that g is continuous at x 0 . Show that the...

Q:

Let f: X Y be differentiable at x0 with derivative Df[x0], and let x be a vector of unit norm (||x|| = 1). Show that the directional derivative of f at x0 in the direction x is the value of the...

Q:

Jr. MATHEMATICS Jr. then dy dx 92. If ya 76. The number of points of non-differentiability for 83. If y1+ and x+y-+ TC in 1) 0 the function f(x)=x|+cos.x+ tan*+ 2)2 -y 4) 3) 1) the interval (-1, 2)...

Q:

Let X be a finite set, let 1 , 2 , ... , A 1 ,A 2 ,...,A n be subsets of X, and let I be a subset of [ ] [n]. Show that the number of elements of X which belong to A i for all iI but for no other...

Q:

3. Find the maximum likelihood estimates of the 2 x 1 mean vector u and the 2 x 2 covariance matrix E based on the random sample 3. 6' 4 X = 4 \4 7/ from a bivariate normal population. [5 + 12 marks]...

Q:

1. (4 points) Let (x) = 1 1 + e x . (a) Show that (x) = 1 (x). (b) Show that the derivative can be written as: d dx(x) = (x)(1 (x))

Q:

1. (4 points) Let (x) = 1 1 + e x . (a) Show that (x) = 1 (x). (b) Show that the derivative can be written as: d dx(x) = (x)(1 (x))

Q:

In Exercises 21-30, calculate the directional derivative in the direction of v at the given point. Remember to use a unit vector in your directional derivative computation.28. 8( X, ), 4 ) -4 29. g...

Q:

X Standard form - Ximera X + -> C ximera.osu.edu/mooculus/calculus1TextbookBySection/implicitDifferentiation/implicitDifferentiation/breakGround H Men Custom Suits... BASEXX... O BERHAS 20... b Big...

Q:

Suppose you find that prices of stocks before large dividend increases show on average consistently positive abnormal returns. Is this a violation of the EMH?

Q:

Siebrecht organized Siebrecht Realty Co., a corporation, and then transferred his building to the corporation in exchange for its stock. The corporation rented different parts of the building to...

Q:

is percentage of receivables used to measure and report impairment

Q:

Storage Technology Corporation (StorageTek) is a manufacturer of computer storage devices. StorageTek continually modifies its existing products and develops new ones. These improvements permit...

Q:

In problem, solve each equation. Express irrational solutions in exact form and as a decimal rounded to 3 decimal places. 8 = 4 x2 2 5x

Q:

In problem, solve each equation. 5 x2+8 = 125 2x

Q:

In problem, use the given function f to: (a) Find the domain of f. (b) Graph f. (c) From the graph, determine the range and any asymptotes of f. (d) Find f -1 , the inverse of f. (e) Find the domain...

Q:

Why are some bonds sold with a premium, some at par value, and some at a discount

Q:

Following is the balance sheet of Finch Company for 2018: FINCH COMPANY Balance sheet Assets Cash Marketable securities Accounts receivable Inventory Property and equipment Accumulated depreciation...

Q:

Following the Digital Marketing at HBS Online article How would you address the concerns about brand dilution and the potential overlap between HBS Online and other programs of the school? How can...