A rectangle is inscribed in a semicircle of radius 2. See the figure. Let P = (x, y) be the point in quadrant I that is a vertex of the rectangle and is on the circle.
(a) Express the area A of the rectangle as a function of x.
(b) Express the perimeter p of the rectangle as a function of x.
(c) Graph A = A(x). For what value of x is A largest?
(d) Graph p = p(x). For what value of x is p largest?
(e) What is the largest area? What is the largest perimeter?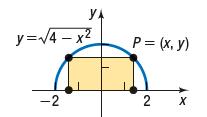

YA y=4-x -2 P = (x, y) 2 X