a. Show that the graph of ex is concave up over every interval of x-values.

b. Show, by reference to the accompanying figure, that if 0

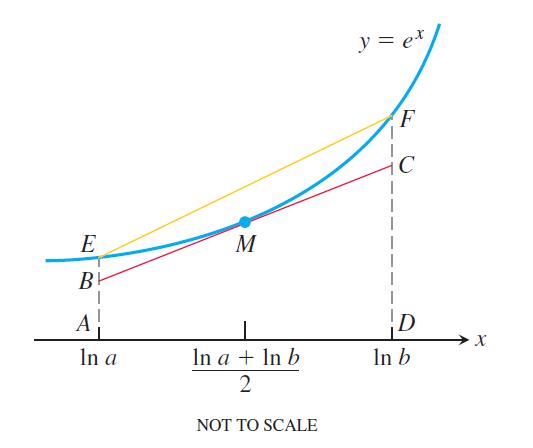
c. Use the inequality in part (b) to conclude that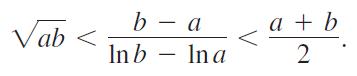

This inequality says that the geometric mean of two positive numbers is less than their logarithmic mean, which in turn is less than their arithmetic mean.

e(Ina+Inb)/2. (Inb - Ina) < < Inb In a et dx < elna + elnb 2 (In b - In a).