A solid of constant density is bounded below by the plane z 0, on the sides by the elliptical cylinder x 2 4y 2 4, and above by the plane z 2 x a Find x and y b Evaluate the integral using integral tables to carry out the final integration with respect to x Then divide M xy by M to verify that z 5 4 Mxy 2 (1 2)4 x 2 x L (1 2)4 x0 z dz dy dx

Question: A solid of constant density is bounded below by the plane z = 0, on the sides by the elliptical cylinder x 2 + 4y

A solid of constant density is bounded below by the plane z = 0, on the sides by the elliptical cylinder x² + 4y² = 4, and above by the plane z = 2 - x.

a. Find x and y.

b. Evaluate the integral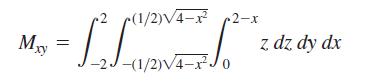 Mxy = 2 (1/2)4-x 2-x [L -(1/2)4-x0 z dz dy dx

using integral tables to carry out the final integration with respect to x. Then divide M_xy by M to verify that z̄ = 5/4.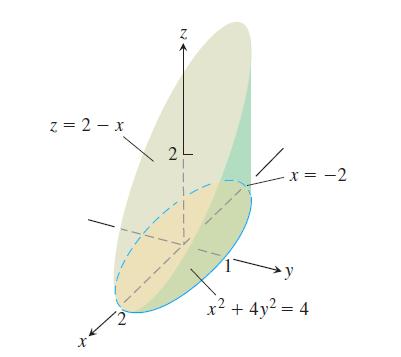

Mxy = 2 (1/2)4-x 2-x [L -(1/2)4-x0 z dz dy dx

Step by Step Solution

★★★★★

3.40 Rating (150 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a The elliptical cylinder can be written in terms of z as z 2 x Solving for x we get x 2 z Substitut... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

A solid trough of constant density is bounded below by the surface z = 4y 2 , above by the plane z = 4, and on the ends by the planes x = 1 and x = -1. Find the center of mass and the moments of...

1. Use double integration in polar coordinates to find the volume of the solid that lies below the surface z = 5 + x y and above the circle x 2 + y 2 = x in the xy-plane. 2. Find the area of the...

Give the limits of integration for evaluating the integral as an iterated integral over the region that is bounded below by the plane z = 0, on the side by the cylinder r = cos , and on top by the...

questions below: Set up the iterated integral for evaluating IIInaz) dz r dr d6 over the given region D. D is the prism whose D base is the triangle in the xy-plane bounded by the x-axis and the...

question below: Use cylindrical coordinates to nd the indicated quantity. Volume of the solid bounded above by the sphere x2 +y2 + z2 = 4, below by the plane 2 = 0, and laterally by the cylinder x2 +...

A solid of constant density is bounded below by the plane z = 0 , above by the cone z = 4 r , r > = 0 , and on the sides by the cylinder r = 1 . Find the center of mass. The center of mass is ( \ bar...

806 Chapter Fifteen OPTIMIZATION: LOCAL AND GLOBAL EXTREMA If f is not continuous or the region R is not closed and bounded, there is no guarantee that f achieves a global maximum or global minimum...

s 1. Find the center of mass of the following plane region with variable density. Describe the distribution of mass in the region: The upper half (y 0) of the y 2 2 disk bounded by the circle x + y...

Mass Question 2, 16.6.9 > HW Score: 0%, 0 of Part 1 of 2 O Points: 0 of 1 Find the mass and center of mass of the thin rod with the following density function. p(x) = 3 + sin x, for OSXSI The mass is...

Several factors are involved in the creation of a confidence interval. Among them are the sample size, the level of confidence, and the margin of error. Which statements are true? a) For a given...

Explain how temperament plays a role in the development of antisocial behavior.

2. Explain the difference between autonomous consumption and induced consumption.

51. In 1984 the country of Morocco in an attempt to determine the average amount of time that tourists spend in that country on a visit tried two different sampling procedures. In one, they...

Problems 113122 are based on previously learned material. The purpose of these problems is to keep the material fresh in your mind so that you are better prepared for later sections, a final exam, or...

Your granny, Sphiwe, wants to enter into a strategic partnership with Alpha Bravo Ltd, Whose Income Statement and Statement of Financial Position are given below. Naturally, she cannot blindly invest...

Shi Import-Export balance sheet allows $300 milliok in debt, $50 million in preferred stock, and $250 million in total common equity: Shi's tax rate is 15%, rd=6%, rps= 7.9%, and rs= 14%. If Shi has...

a. Service revenue accrued, $700. Review the worksheet b. Office supplies used, $300. (Assume that Best Jobs Employment Service dehits an asset account when supplles are purchased) Review the...