a. Use the method of Exercise 7 to find N for the curve r(t) = t i + (1/3)t³ j when t 0.

b. Calculate N for t ≠ 0 directly from T using Equation (4) for the curve in part (a). Does N exist at t = 0? Graph the curve and explain what is happening to N as t passes from negative to positive values.

Data from in Exercise 7

a. Show that n(t) = -g′(t)i + ƒ′(t)j and -n(t) = g′(t)i - ƒ′(t)j are both normal to the curve r(t) = ƒ(t)i + g(t)j at the point (ƒ(t), g(t)).

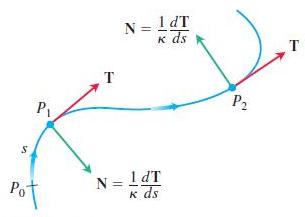
To obtain N for a particular plane curve, we can choose the one of n or -n from part (a) that points toward the concave side of the curve, and make it into a unit vector. (See Figure 13.19.) Apply this method to find N for the following curves.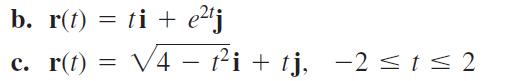

In Figure 13.19

b. r(t) = ti + etj c. r(t) r(t) = 4 ti + tj, 2 t 2