Question: a. Use Theorem 8 to show that b. From Example 5, show that c. Explain why taking the first M terms in the series in
a. Use Theorem 8 to show that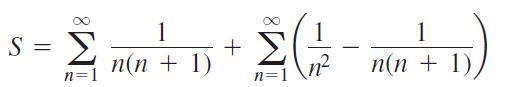
b. From Example 5, show that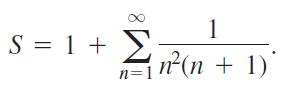
c. Explain why taking the first M terms in the series in part (b) gives a better approximation to S than taking the first M terms in the original series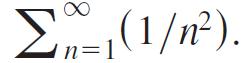
d. We know the exact value of S is π2/6. Which of the sums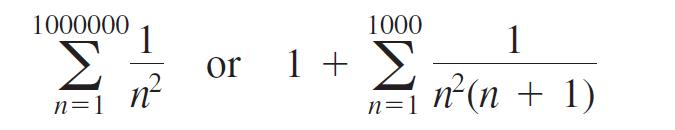
gives a better approximation to S?

S = n=1 1 n(n + 1) + n=1 n(n + 1)
Step by Step Solution
3.47 Rating (154 Votes )
There are 3 Steps involved in it
ANSWER a Lets start by simplifying the expression using the provided formulas S n1 to 1nn 1 n1 to 1n2 1nn 1 Using the telescoping series technique we can simplify the second sum as follows n1 to 1n2 1nn 1 n1 to 1n2 1nn 1 n1 to 1n2 1n 1n 1 Now lets split the first sum into two separate sums S n1 to 1nn 1 n1 to 1n2 1n 1n 1 n1 to 1nn 1 n1 to 1n2 n1 to 1n n1 to 1n 1 Using Theorem 8 we can simplify the expression further S 1 n1 to 1n ... View full answer

Get step-by-step solutions from verified subject matter experts


