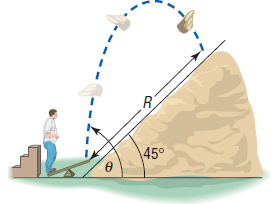
An object is propelled upward at an angle , 45 < < 90, to the horizontal with an initial velocity of 0 feet

An object is propelled upward at an angle θ, 45° 0 feet per second from the base of a plane that makes an angle of 45°with the horizontal. See the illustration. If air resistance is ignored, the distance R that it travels up the inclined plane is given by the function

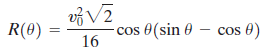
(a) Show that

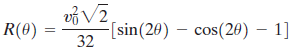
(b) In calculus, you will be asked to find the angle θ that maximizes R by solving the equation

sin(2θ) + cos(2θ) = 0

Solve this equation for u.

(c) What is the maximum distance R if υ₀ = 32 feet per second?

(d) Graph R = R(θ), 45° ≤ θ ≤ 90°, and find the angle θ that maximizes the distance R. Also find the maximum distance. Use υ₀ = 32 feet per second. Compare the results with the answers found earlier.

R(0) cos 0(sin 0 16 cos 0) 45