By eliminating from the ideal projectile equations show that x 2 + (y + gt 2 /2) 2 = 0 2 t 2

By eliminating α from the ideal projectile equations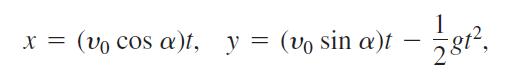

show that x² + (y + gt²/2)² = ν₀² t². This shows that projectiles launched simultaneously from the origin at the same initial speed will, at any given instant, all lie on the circle of radius ν₀t centered at (0, -gt²/2), regardless of their launch angle. These circles are the synchronous curves of the launching.

x = (vo cos a)t, y = (vo sin a)t - 281