Consider the function f(x) = x^3/2 with the solution point (4, 8).

(a) Use a graphing utility to graph f. Use the zoom feature to obtain successive magnifications of the graph in the neighborhood of the point (4, 8). After zooming in a few times, the graph should appear nearly linear. Use the trace feature to determine the coordinates of a point near (4, 8). Find an equation of the secant line S(x) through the two points.

(b) Find the equation of the line T(x) = f′(4)(x − 4) + f(4) tangent to the graph of f passing through the given point. Why are the linear functions S and T nearly the same?

(c) Use a graphing utility to graph f and T on the same set of coordinate axes. Note that T is a good approximation of f when x is close to 4. What happens to the accuracy of the approximation as you move farther away from the point of tangency?

(d) Demonstrate the conclusion in part (c) by completing the table.

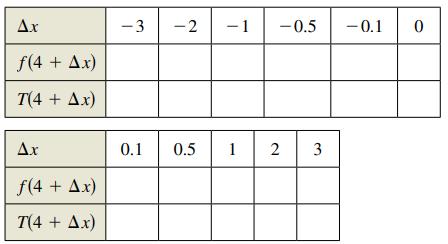
f(4 + .x) (4 + .x) f(4 + .x) (4 + .x) -3 -2 - 1 0.1 0.5 1 -0.5 2 3 -0.1 0