Consider the graph of the function f(x) = x² − x − 12 (see figure).

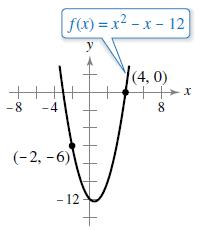
(a) Find the equation of the secant line joining the points (−2, −6) and (4, 0).

(b) Use the Mean Value Theorem to determine a point c in the interval (−2, 4) such that the tangent line at c is parallel to the secant line.

(c) Find the equation of the tangent line through c.

(d) Use a graphing utility to graph f, the secant line, and the tangent line.

++ -8 -4 f(x)=x-x-12 (-2,-6) - 12 y E (4,0) 8 X