Question: Each of these extreme value problems has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme

Each of these extreme value problems has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint.

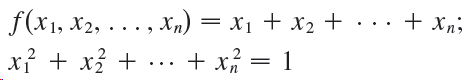
+ Xn f(x1, x2, ..., Xn) = x1 + x2 + + x = 1 xỉ + x + ... + xỉ = 1

+ Xn f(x1, x2, ..., Xn) = x1 + x2 + + x = 1 x + x + ... + x = 1

Step by Step Solution

★★★★★

3.39 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

fx1 x2 n X1 X2 xn gx1 x2 xn x x x 1 1 1 1 2... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Q:

Use Lagrange multipliers to find the maximum value of z = x + 2xy subject to the constraint x + 2y = 5

Q:

Use Lagrange multipliers to find the maximum and the minimum of ((x, y) = xy subject to the constraint x2 + y2 = 1.

Q:

(a) Use Lagrange multipliers to find the maximum value of z = 4xy subject to the constraint x + 2y = 40 State the associated values of x, y and l. (b) Repeat part (a) when the constraint is changed...

Q:

3-16 Each of these extreme value problems has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given...

Q:

Please write down the answer by hand on a paper, that would help me understand it more easily 14.8 Lagrange Multipliers Each of these extreme value problems has a solution with both a maximum value...

Q:

Each of these extreme value problems has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint....

Q:

Each of these extreme value problems has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint....

Q:

Each of these extreme value problems has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint....

Q:

Each of these extreme value problems has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint....

Q:

Each of these extreme value problems has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint....

Q:

The precise mechanism of ammonia toxicity to the brain is not known. Speculate on a possible mechanism, based on possible effects of ammonia on levels of key intermediates in energy generation.

Q:

: Four steps to prepare a production cost report MIXING DEPARTMENT Units Work in process, June 1 Direct materials: 100% complete Conversion costs: 70% complete Units started into production during...

Q:

9. Feagler plcs current income taxes payable related to its taxable income for 2025 is 460,000. In addition, Feaglers deferred tax asset decreased 20,000 during 2025. What is Feaglers income tax...

Q:

1.15. "Because the public can see whether a central bank hits its monetary targets almost immediately, whereas it takes time before the public can see whether an infla- tion target is achieved,...

Q:

Find all values of x in the interval [0, 2] that satisfy the equation. 2 cos x + sin 2x = 0

Q:

Find all values of x in the interval [0, 2] that satisfy the equation. |tan x | = 1

Q:

If u(x) = f (x) + it(x) is a complex-valued function of a real variable x and the real and imaginary parts f (x) and g(x) are differentiable functions of x, then the derivative of u is defined to be...

Q:

Hoover Roofing has existing assets that generate $6 in earnings per share. If the firm does not invest except to maintain existing assets, EPS is expected to remain constant at $6 a year. However,...

Q:

The federal election is scheduled to be held in the rst half of 222. The 2019 election showed divides between men and women and among voters from different age groups. 43.3 % voters in the 18-24 age...

Q:

Suppose a 10-year, $1,000 bond with a 12% coupon rate and semiannual coupons is trading for a price of $1,157.11. a. What is the bond's yield to maturity (expressed as an APR with semiannual...