Question: Find the linearization L(x, y) of the function (x, y) at the point P 0 . Then find an upper bound for the magnitude of

Find the linearization L(x, y) of the function ƒ(x, y) at the point P₀. Then find an upper bound for the magnitude of the error E in the approximation ƒ(x, y) ≈ L(x, y) over the rectangle R.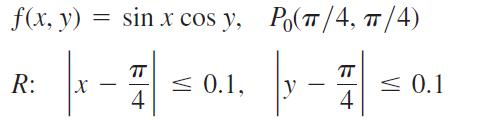 f(x, y) = sin x cos y, Po(/4, /4) HR 4 R:

f(x, y) = sin x cos y, Po(/4, /4) HR 4 R: X - 0.1, y - TT = 4 0.1

Step by Step Solution

★★★★★

3.28 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

We are given the function x y 2x2 3y2 xy and the point P01 2 The linearization of x y at P0 is given ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

1. Muy Bueno Bakery sells its special chocolate cake for $35. The total cost to produce the cake is $26. Of this amount, $4 per unit is selling costs. The total variable cost is $17. The desired...

Find the linearization L(x, y) of the function (x, y) at the point P 0 . Then find an upper bound for the magnitude of the error E in the approximation (x, y) L(x, y) over the rectangle R. f(x, y) =...

Find the third Taylor polynomial P3(x) for the function f (x) = (x 1) ln x about x0 = 1. a. Use P3(0.5) to approximate f (0.5). Find an upper bound for error |f (0.5) P3(0.5)| using the error...

webwork / math213rdong / homework06 / 6 Homework06: Problem 6 Previous Problem Problem List Next Problem (3 points) Find equations of the tangent plane and normal line to the surface x - 5y? | 12...

Find the equation of the tangent plane to the surface z = 4y 9 at the point (3,-3,-45). Z= Note: Your answer should be an expression of x and y: e.g. "3x - 4y +6" Question 2 Find the equation of the...

Find the linearization L x y of the function at each point 2 f x y x y 1 a 3 0 b 1 3 a L x y Type an exact answer using it as needed

tangent planes (1 point) Let f(x, y) = 2x' + 3xy + 2y + 3x - 3y+2. Find the linearization L(x, y) of f(x, y) at the point (1, -1). L(x, y) = Find an upper bound for the magnitude | E| of the error in...

Find the fourth Taylor polynomial P4(x) for the function f (x) = x(ex)2 about x0 = 0. a. Find an upper bound for |f (x) P4(x)|, for 0 x 0.4. b. Approximate c. Find an upper bound for the error in...

Tangent Planes and Linear Approximations 10 Find an equation of the tangent plane to the given surface at the specified point. z = In (x - 2y), (3, 1, 0) Explain why the function is differentiable at...

1 Find the linearization L(x,y) of the function f(x,y) = x" -7xy +7 at P (4,4). Then find an upper bound for the magnitude E of the error in the approximation f(x,y) ~ L(x,y) over the rectangle R: |x...

Singapore does an excellent job of managing population health by identifying patients needs and allocating the right resources to these patients. What did they develop to assist with this management...

Find the following limit without using a graphing calculator or making a table. [(t + 5)t-/2] t-25

Homestead land sales added up to 5 0 million acres, however, over 1 0 0 million acres were given away to railroad companies free of charge! True or false

=+calculate estimates of any probabilities that are relevant to your justification.

(a) Verify that the series converges, (b) Use a graphing utility to find the indicated partial sum S n and complete the table, (c) Use a graphing utility to graph the first 10 terms of the sequence...

Determine the convergence or divergence of the series using any appropriate test from this chapter. Identify the test used. o -n/3 n=1

Determine the convergence or divergence of the series using any appropriate test from this chapter. Identify the test used. n=1 4 n2

Problem 4-238 (LO 4-5] On December 31, 2018, Ditka Inc, had Retained Earnings of $280,800 before its closing entries were prepared and posted. During 2018, the company had service revenue of $181100...

Present Value of Bonds Payable; Premium Moss Co. issued $740,000 of four-year, 13% bonds, with interest payable semiannually, at a market (effective) interest rate of 11%. Determine the present value...

need help with part c! in last picture. Novak's gross earnings for the week were $1,850, his federal income tax withholding was $334, and his FICA total was $141. There were no state income taxes....