Find the unit tangent vector to the involute of the circle at the point P(x, y). (See Exercise 19)

Data from in Exercise 19

If a string wound around a fixed circle is unwound while held taut in the plane of the circle, its end P traces an involute of the circle. In the accompanying figure, the circle in question is the circle x² + y² = 1 and the tracing point starts at (1, 0). The unwound portion of the string is tangent to the circle at Q, and t is the radian measure of the angle from the positive x-axis to segment OQ. Derive the parametric equations x = cos t + t sin t, y = sin t - t cos t, t > 0 of the point P(x, y) for the involute.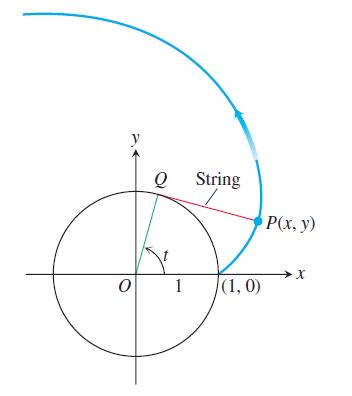

y 0 QString 1 (1, 0) P(x, y) X