Question: Find the work done by each field along the paths from (0, 0, 0) to (1, 1, 1) in Exercise 1. F = 2xyi +

Find the work done by each field along the paths from (0, 0, 0) to (1, 1, 1) in Exercise 1.

F = 2xyi + j + x²k

Data from Exercise 1

The accompanying figure shows two polygonal paths in space joining the origin to the point (1, 1, 1). Integrate ƒ(x, y, z) = 2x - 3y² - 2z + 3 over each path.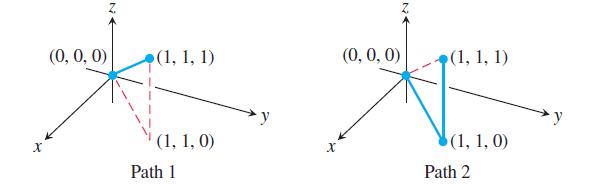 NE (0, 0, 0) (1, 1, 1) (1, 1, 0) Path 1

NE (0, 0, 0) (1, 1, 1) (1, 1, 0) Path 1 (0, 0, 0) (1, 1, 1) (1, 1, 0) Path 2

Step by Step Solution

★★★★★

3.35 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To find the work done by the field along each path we need to evaluate the line integral of the field vector F along the paths The line integral is gi... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Find the work done by each field along the paths from (0, 0, 0) to (1, 1, 1) in Exercise 1. F = 2xyi + x 2 j + k Data from Exercise 1 The accompanying figure shows two polygonal paths in space...

The accompanying figure shows two polygonal paths in space joining the origin to the point (1, 1, 1). Integrate (x, y, z) = 2x - 3y 2 - 2z + 3 over each path. NE (0, 0, 0) (1, 1, 1) (1, 1, 0) Path 1...

In Problems 1-3, find the work done by the force field F in moving a particle along the curve C? 1. F(x,y) = (x3 - y3)I + xy2j; C is the curve x = t2, y = t3, -1 ( t ( 0? 2. F(x, y) = exi - e-yj; C...

Work and Circulation In ExeRRcciissee 3 3 5 5 , find the work done by each field along th paths from ( 0 , 0 , 0 ) to ( 1 , 1 , 1 ) in Exercise 1 . 3 5 . F = 2 xyi + j + x 2 k

An object, attached to a frame A, is subjected to the forces and moments given relative to the reference frame. If the object was moved along its frame n-axis a distance of 0.1m, about the a-axis for...

Please answer in MATLAB CODING, I NEED CODING FOR THIS QUESTION ONLY NOT MANUAL CALCULATION. If you are not going to answer as a MATLAB, dont touch it. I will report to Chegg that you have done...

Please shows work (1 point) Evaluate the line integral x'z ds, where C is the line segment from (0, 2, 5) to (4, 8, 3).(1 point) Evaluate the line integral 6xy ds, where C is the right half of the...

Please thanks! (1 point) Let F be the radial force field F(x, y) = xi + yj. Find the work done by this force along the following two curves, both which go from (0, 0) to (2, 4). (Use the Fundamental...

Let F be the radial force field F = ci + yj. Find the work done by this force along the following two curves, both of which go from (0, 0) to (9, 81). (Compare your answers!) A. If C1 is the...

(1 point) Let F be the radial force field F : mi | yj. Find the work done by this force along the following two curves, both which go from (O, O) to (2, 4). (Compare your answers!) A. IfC'1 is the...

Book Barn Inc. issued $600,000 of 9%, 10 year bonds on June 30, 2015, for $562,500. This price provided a yield of 10% on the bonds. Interest is payable semi annually on December 31 and June 30....

The housing market in Kabul is heavily dependent on two main factors; supply and demand. Both play a major role in determining an equilibrium price for both sellers and buyers in the real estate...

23. Teenage Cell Phone Use. Pew Research Center is a nonpartisan polling organization that provides information about issues, attitudes, and trends shaping America. In a poll, Pew researchers found...

Suppose in Example 2.31 that those choosing their own hats depart, while the others (those without a match) put their selected hats in the center of the room, mix them up, and then reselect. Also,...

Problems 113 122. The purpose of these problems is to keep the material fresh in your mind so that you are better prepared for later sections, a final exam, or subsequent courses such as calculus. X...

In Problems 91114, solve each equation. log 3 3x = 1

Show that log a (1/N) = log a N, where a and N are positive real numbers and a 1.

may Following charges P write the likely transactions that result in the the accounting equation. (a) increase in capited, 10,000 increase in motor vehicle, 2500 and increase in bank 2,500. (8)...

The Juicy Company manufactures flavored organic lemonade. Management is ready to close the books for the end of the 1 st quarter in 2013 and your supervisor has presented you with fallowing...

Sultan Company uses an activity-based costing system. At the beginning of the year, the company made the following estimates o cost and activity for its five activity cost pools: Required: 1. Compute...