Find the work done by F = e^yzi + (xze^yz + z cos y)j + (xye^yz + sin y)k over the following paths from (1, 0, 1) to (1, π/2, 0).

a. The line segment x = 1, y = πt/2, z = 1 - t, 0 ≤ t ≤ 1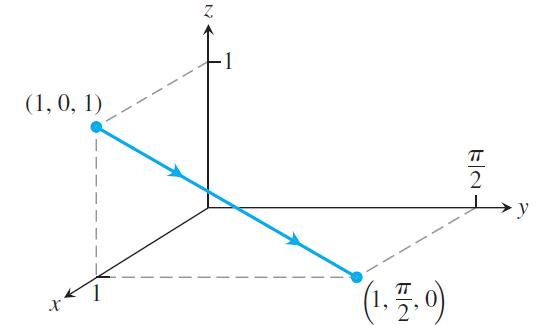

b. The line segment from (1, 0, 1) to the origin followed by the line segment from the origin to (1, π/2, 0)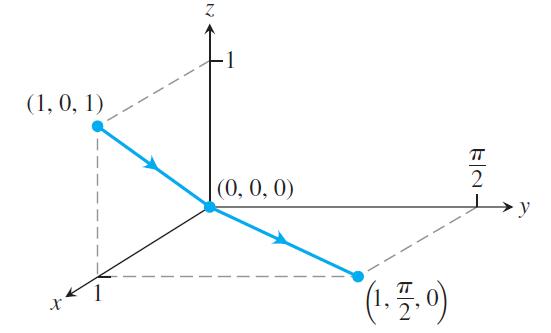

c. The line segment from (1, 0, 1) to (1, 0, 0), followed by the x-axis from (1, 0, 0) to the origin, followed by the parabola y = πx²/2, z = 0 from there to (1, π/2, 0)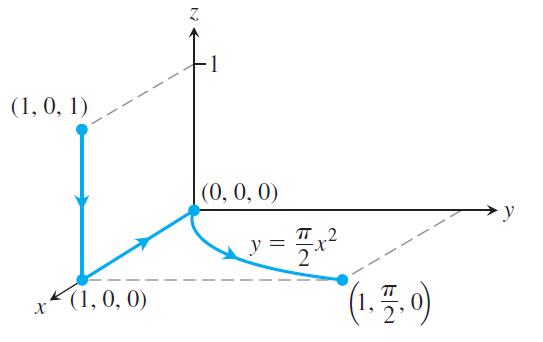

(1, 0, 1) X N 1 (1,7,0) 2 y