If x is a rational number, then x can be written in a unique way as a quotient of integers m/n where n > 0 and m and n have no common factors greater than 1. (We say that such a fraction is in lowest terms. For example, 6/4 written in lowest terms is 3/2.) Let ƒ(x) be defined for all x in the interval [0, 1] by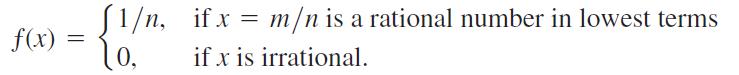

For instance, ƒ(0) = ƒ(1) = 1, ƒ(1/2) = 1/2, ƒ(1/3) = ƒ(2/3) = 1/3, ƒ(1/4) = ƒ(3/4) = 1/4, and so on.

a. Show that ƒ is discontinuous at every rational number in [0, 1].

b. Show that ƒ is continuous at every irrational number in [0, 1].

c. Sketch the graph of ƒ. Why do you think ƒ is called the “ruler function”?

f(x) = = [1/n, if x = m/n is a rational number in lowest terms 10, if x is irrational.