Question: In problem, find the domain of each rational function. R(x) = 3(x - x - 6) 2 4(x - 9)

In problem, find the domain of each rational function.

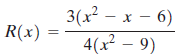
3(x² – x - 6) R(x): 4(x – 9) 9)

R(x) = 3(x - x - 6) 2 4(x - 9)

Step by Step Solution

★★★★★

3.53 Rating (167 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

In the denominator qx 4x 2 9 4... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Q:

In problem, find the domain of each rational function. R(x) = x/x 4 - 1

Q:

In problem, find the domain of each rational function. Find any horizontal, vertical, or oblique asymptotes. x + 3x + 2 (x + 2) |R(x)

Q:

In problem, find the domain of each rational function. H(x) = 3x 2 + x/x 2 + 4

Q:

In Problems 1526, find the domain of each rational function. R (x) || X x - 64

Q:

Question 1 0.1 pts State whether the function is a polynomial function or not. If it is, give its degree. If it is not, tell why not. f(x) = 16x4 + 9x3 + 6 0. Yes; degree4 O. No; the last term has no...

Q:

Find the domain of the rational function n x) = 8 X ( x + 9 ) ( x + 6 ) 1 1 ) Given the function f ( x ) = - 2x 2 + 4 x - 3 if x = 1 What is f ( x ) what is on the point on the graph Of f 2 18 Find f...

Q:

In problem, find the domain of each rational function. G(x) = 6 (x + 3) (4 - x)

Q:

In problem, find the domain of each rational function. Find any horizontal, vertical, or oblique asymptotes. R(x) = x + 4 x-2

Q:

In problem, find the domain of each rational function. Find any horizontal, vertical, or oblique asymptotes. R(x) = x x - 1

Q:

In Problems 1526, find the domain of each rational function. H(x) -4x (x - 2) (x + 4)

Q:

If two separate partnership LLCs with the same owners established another new business and share the revenue, what accounting procedures need to be done? For example, First Company A is a retail...

Q:

Diane owns and manages a successful clothing store in Dallas. Just prior to the graduation of her brother, Cameron, they investigated the possibility of opening another store in Atlanta for Cameron...

Q:

A bond that makes no coupon payments and is initially priced at a deep discount is called a Blank _ _ _ _ _ _ . Multiple choice question. stripped bond convertible bond low - yield bond callable bond...

Q:

Rearrange Formula 14.2 into its price/earnings form.What does this say about the earnings/price yield for firms with no PVGO? About firms with positive PVGO? Negative PVGO?

Q:

People often respond to survey questions without any knowledge of the subject matter. A common example of this is the discussion on banning dihydrogen monoxide. The Centers for Disease Control (CDC)...

Q:

In October 2014, there was an Ebola breakout in West Africa. At the time, there was no vaccine for the virus, however, there were some experimental drugs that had not yet been approved for humans....

Q:

In October 2014, there was an Ebola breakout in West Africa. At the time, there was no vaccine for the virus, however, there were some experimental drugs that had not yet been approved for humans....

Q:

At the beginning of the month, the Forming Department of Martin Manufacturing had 22,000 units in inventory, 30% complete as to materials, and 10% complete as to conversion. During the month the...

Q:

Cash fow to the waman under an interest-only loan, in which Poryi will pay the annual intecest expense each year and pay the principal back at the end of the contract What is the amount of payment...

Q:

A project will produce operating cash flows of $45,000 a year for four years. During the life of the project, inventory will be lowered by $30,000 and accounts receivable will increase by $15,000....