In Problems 90–96, use Descartes’ method from Problem 89 to find an equation of the tangent line to each graph at the given point.

x² − y² = 3; at (2, 1)

Data from problem 89

Descartes’ method for finding tangent lines depends on the idea that, for many graphs, the tangent line at a given point is the unique line that intersects the graph at that point only. We use his method to find an equation of the tangent line to the parabola y = x² at the point (2, 4). See the figure.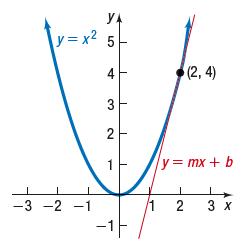

First, an equation of the tangent line can be written as y = mx + b. Using the fact that the point (2, 4) is on the line, we can solve for b in terms of m and get the equation y = mx + (4 − 2m). Now we want (2, 4) to be the unique solution to the system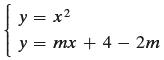

From this system, we get x² − mx + (2m − 4) = 0. Using the quadratic formula, we get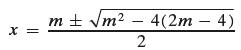

To obtain a unique solution for x, the two roots must be equal; in other words, the discriminant m² − 4(2m − 4) must be 0. Complete the work to get m, and write an equation of the tangent line.

Transcribed Image Text:

YA y=x² 5 -3 -2 -1 4 3 2 1 -1-- (2,4) y = mx + b 12 3 x