Leibnizs Rule says that if is continuous on [a, b] and if u(x) and (x) are differentiable functions of x whose values lie in

Leibniz’s Rule says that if ƒ is continuous on [a, b] and if u(x) and ν(x) are differentiable functions of x whose values lie in [a, b], then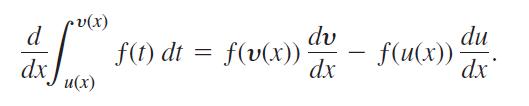

Prove the rule by setting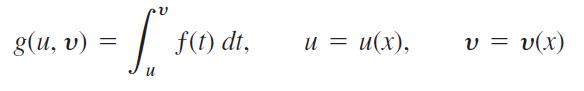

and calculating dg / dx with the Chain Rule.

d dx v(x) u(x) f(t) dt = f(v(x)) dv dx - du dx - f(u(x)).