Let C be a curve given by y f (x) Let K be the curvature (K 0) at the point P(x 0 , y 0 ) and let Show that the coordinates (, ) of the center of curvature at P are (, ) (x 0 f '(x 0 )z, y 0 z) z Z 1 f'(x)

Question: Let C be a curve given by y = f (x). Let K be the curvature (K 0) at the point P(x 0 ,

Let C be a curve given by y = f (x). Let K be the curvature (K ≠ 0) at the point P(x₀, y₀) and let

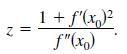
z = Z 1 + f'(x)

Show that the coordinates (α, β) of the center of curvature at P are (α, β) = (x₀ - f'(x₀)z, y₀ + z).

z = Z 1 + f'(x)

Step by Step Solution

★★★★★

3.30 Rating (162 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To show that the coordinates of the center of curvature at point Px0 y0 are x0 fx0z y0 z we need to use the properties of curvature and the definition of the center of curvature The curvature K at a p... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Let C be a smooth C2 arc with parametrization (É¸, [a, b]), and suppose that s = ï¬(t) is given by (2). The natural parametrization of C is the pair (v, [0, L]), where v(s) =...

Ammonium nitrate decomposes to N2O and water in temperaturesbetween 250C and 300C. Write a balanced chemical reactiondescribing the decomposition of ammonium nitrate, and calculate thestandard heat...

Let C be a smooth arc and gk : C R be continuous for n N. a) If gk g uniformly on C, prove that C gk ds C g ds as k . b) Suppose that {gk} is pointwise monotone and that gk g pointwise on C as...

Use the following information to find the center of curvature for the curve at the given point. Let C be a curve given by y = f(x). Let K be the curvature (K # 0) at the point P(X, yo) and let Z = 1...

SPIRAT GOING IS A-NEHISI COATES. EGOING 748 CHAPTER 14 CALCULUS OF VECTOR-VALUED FUNCTIONS functions: 14. Match the space curves in Figure 7 with the following vector-valued 18. Describe the...

Math 107 Final Examination Spring, 2017 Answer: Si 24',\" 4-7 1* L/ Work. 25 {a I .7 {3; r .. "5 f 5: Ci? m\" I i (a) 2% (b) 73+\" 26 Work for part (a) and for part (b): (Gr \"my yr : mgr: \\ JE/...

In Hermite interpolation we are looking for a polynomial p(x) (of degree 2n + 1 or less) such that p(x) and its derivative p'(x) have given values at n + 1 nodes. (More generally, p(x), p'(x), p"(x),...

(i) (5 marks) Let F(x, y, z) = (sin(y), x cos(y) + cos(z), -ysin (z)). Let C be the curve given by Y130 CUHK Examination ENGGH130 CUHK Examination ENGGI130 CUIK Examin CG1130 CUHK Examination ANGG130...

Evaluate the integral 1Z 0 ex+1 x + 1 + 3x + 4 x2 + 3x + 2! dx. b) Given that F(x) = 1+x2 Z 1+x sint3tant dt, nd F0(1). 2. Determine the type of each of the following improper integrals and determine...

C We Determine The Work ! X G Let - FB C myopenmath.com/assess2/7cid=110062&aid =7889798#/full/page/3 My MyOpenMath C Homework Helper 41 Microsoft Teams - P... DO Math Problem Solver C Textbook...

Based on information contained in charts in this chapter, specify an approximate height for a vertical flat plate and diameter of a horizontal cylinder for which the simplified equations of Table 7-2...

Based on the defining and understanding of audit sampling: 1. Why it is important for the auditor to select and audit reasonable numbers of transactions instead of taking auditing the whole...

Question content area top Part 1 Recording Social Security Taxes Payable would be an example of a ( n ) : Question content area bottom Part 1 A . deferred expense. B . deferred revenue. C . accrued...

18. Craig has been diagnosed with schizophrenia and has been prescribed Thorazine to reduce delusions and hallucinations. Which of the following side effects might Craig experience from taking this...

The utility function U = (x, y) is a measure of the utility (or satisfaction) derived by a person from the consumption of two products x and y. The utility function for two products is (a) Determine...

The value of an investment of $1000 earning 6% compounded annually is where I is the annual rate of inflation and R is the tax rate for the person making the investment. Calculate V 1 (0.03, 0.28)...

If is a function of x and y such that xy and yx are continuous, what is the relationship between the mixed partial derivatives? Explain.

On 3/1/20, Ollie Co. paid $840 for an advertisement to run in the Seattle Times every month for 12 months (3/1/20 - 2/28/21). Assuming Ollie Co. makes adjusting entries once a year and their fiscal...

Presented below is information related to Pharoah Co., owned by D. Davis, for the month of January 2024. Ending inventory per perpetual records Ending inventory actually on hand Cost of goods sold...

Following is a list of account balances of Nabers Delivery Services as of December 31, after the first year of operations Accounts Receivable Accounts Payable Salaries Expense Repairs Expense Truck...