Question: Let g be a function that is differentiable throughout an open interval containing the origin. Suppose g has the following properties: i. ii. iii. a.

Let g be a function that is differentiable throughout an open interval containing the origin. Suppose g has the following properties:


i.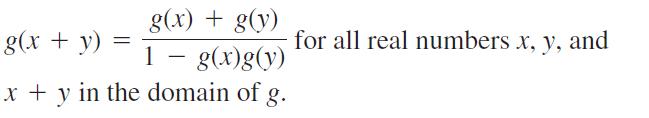g(x) + g(y) 1 - g(x)g(y) x + y in the domain


ii.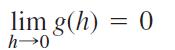of g. g(x + y) = for all real numbers x, y,


iii.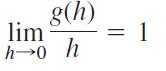and


a. Show that g(0) = 0.


b. Show that g′(x) = 1 + [g(x)]2.


c. Find g(x) by solving the differential equation in part (b).

g(x) + g(y) 1 - g(x)g(y) x + y in the domain of g. g(x + y) = for all real numbers x, y, and

Step by Step Solution

★★★★★

3.43 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a To show that g0 0 we can use property i Letting x y 0 we have g0 0 g0 g01 g0 g0 Simplifying the ri... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Q:

Suppose that I is an open interval containing a, and that f, g, h : I R. Decide which of the following statements are true and which are false. Prove the true ones and provide counterexamples for...

Q:

Suppose that the functions and g are defined throughout an open interval containing the point x 0 , that is differentiable at x 0 , that (x 0 ) = 0, and that g is continuous at x 0 . Show that the...

Q:

Use the result of Exercise 21 to show that the following functions are differentiable at x = 0. Data from in Exercise 21 Suppose that the functions and g are defined throughout an open interval...

Q:

please only solve question number 9 only [IV, $4] FUNCTIONS DEPENDING ON DISTANCE FROM ORIGIN 109 110 THE CHAIN RULE AND THE GRADIENT [IV, $4] IV, $4. EXERCISES 7. Parametrizatione (x*/a*) + (y*/b')...

Q:

All questions. 05:50:42 VA; 25% ' ASSIGNMENTNM1.pdf IQ 0+ Numerical Methods-Assignment-l Mathematical Prelimanaries, Taylor's Theorem, Order of Convergence (1) Let L be a real number and let {an} be...

Q:

9. Let f be a differentiable function with / (2) = 3 and f "(2) - -5, and let g be the function defined by (x) = x/(x). Which of the following is an equation of the line tangent to the graph of g at...

Q:

I need perfect score, need complete solution each step by step pls i will rate helpful: INTRODUCTION In the previous lesson, we presented and illustrated the limit theorems. We started recalling...

Q:

Non-Calculator Lab S-2 1. The graph of the function f, consisting of three line segments and a quarter of a circle, is shown above. Let g be the function defined by g(x) = 2x + Sf(t)dt a. Find the...

Q:

Need some help with these problems.Ignore the little piece of the graph at the topthanks in advance!! 18. Identify the open interval(s) on which the function f(x) = x - x-12 is increasing. (A) (-00,...

Q:

Let a R and let f and g be real functions defined at all points x in some open interval containing a except possibly at x = a. Decide which of the following statements are true and which are false....

Q:

A diffuse, gray radiation shield of 60-mm diameter and emissivities of ? 2, i = 0.01 and ? 2, o = 0.1 on the inner and outer surfaces, respectively, is concentric with a long tube transporting a hot...

Q:

Access eBays, January 31, 2014, filing of its 10-K report for the year ended December 31, 2013, at www.SEC.gov. Required 1. What is the amount of eBays net accounts receivable at December 31, 2013,...

Q:

a process cost accounting system is most appropraite when similar products are mass produced

Q:

=+b. Would you prefer a significance level of .1 or .01 for your test? Explain.

Q:

Determine whether each infinite geometric series converges or diverges. If it converges, find its sum. 9. 3 4

Q:

Determine whether each infinite geometric series converges or diverges. If it converges, find its sum. 5 k-1 5. 5 4 k=1

Q:

Determine whether each infinite geometric series converges or diverges. If it converges, find its sum. k-1 (2, k=1

Q:

Vincent lives with his daughter, June. Vincent received $5,500 in social security benefits. He used $2,400 for rent , $1,000 for food, $1,500 for recreation, $500 for the doctor, and $100 for...

Q:

Which is a true statement: a. Under US GAAP, a company will always have to impair a building if a triggering even occurs and the fair value is less than the book value. b. unless it is sold, the book...

Q:

Stiedemann LLC had original sales and cost data for the month of December as follows: Calculate the contribution margin ratio for Stiedemann LLC (Round answers to two decimal places). 57.89% 42.11%...