Question: Let where f is continuous for all real t. Find (a) G(0), (b) G'(0), (c) G''(x), (d) G''(0). G(x) = S[$ f* 0 f(1) f(t)

Let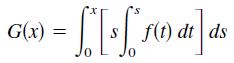G(x) = S[$ f* 0 f(1) f(t) dt dswhere f is continuous for all real t. Find


(a) G(0),


(b) G'(0),


(c) G''(x), 


(d) G''(0).

G(x) = S[$ f* 0 f(1) f(t) dt ds

Step by Step Solution

★★★★★

3.49 Rating (159 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

ANSWER To solve this problem we will use the Fundamental Theorem of Calculus and the Chain Rule for ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Q:

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-6. On December 12, Irene purchased the building where her store is located. She paid...

Q:

Emily Jackson (Social Security number 765-12-4326) and James Stewart (Social Security number 466-74-9932) are partners in a partnership that owns and operates a barber shop. The partnership's first...

Q:

Carol Harris, Ph.D, CPA, is a single taxpayer and she lives at 674 Yankee Street, Durham, NC 27409. Her Social Security number is 793-52-4335. Carol is an Associate Professor of Accounting at a local...

Q:

Can you please complete those questions. Thank you 1. Suppose that f and g are differentiable functions and let h(x) = f (x)g(x) (a) Show that h = f g1 (f g + f gln f ) (b) If f (x) = b (where b is a...

Q:

Explain the difference between an absolute minimum and a local minimum. O A function f has an absolute minimum at x = c if f(c) is the smallest function value on the entire domain of f, whereas f has...

Q:

Find all of the critical points of the function A. x = 0 f (x) = 13x| B. x - 3, x - -3 C. x - 3, x = 0, X - -3 f() - 13x) D. If (x) has no critical points. 2 -2\fFind the interval (s) where the...

Q:

Suppose that a a) If f is continuous and nonnegative on [a, b] and g : [a, b] [a, b] is differentiable and increasing on [a, b], then is increasing on [a, b]. b) If f and g are differentiable on [a,...

Q:

Let d, f, and g be defined as follows. . d: {0, 1)4 -> {0, 1)4. d(x) is obtained from x by removing the second bit and placing it at the end. For example, f(1011) = 1110. . f: (0, 1]4 -> {0, 1]4....

Q:

Fraction of hosts infected Case Study 2 Hosts, Parasites, and Time-Travel 0.8 0.6 0.4 0.2 0 Past Contemporary Future Time Figure \u00031 Horizontal axis is the time from which the parasite was taken,...

Q:

Unit 2: Derivatives Instructions There are 16 questions in this Assessment Opportunity. Show all work for each question. 1. Find the derivative of the following. a. f(x) =13x* -7x3 +5x3+11x+75 b....

Q:

How might investors protect themselves from being the victims of a Ponzi Scheme? What are the controls and triggers which can be implemented to ensure your investments and assets are being managed in...

Q:

Let X Geom(p). Let s 0 be an integer. a. Show that P(X > s) = (1 p)s. b. Let t 0 be an integer. Show that P(X > s + t | X > s) = P(X > t). This is called the lack of memory property. c. A penny...

Q:

A cost that does not change at any level of activity within the relevant range is a cost .

Q:

=+ If a correlation coefficient is reported, is it accompanied by a test of significance? Are the results of the test interpreted properly?

Q:

In Exercises find the derivative of the function. 4 g(x) = log21-x

Q:

In Exercises find the derivative of the function. f(t) = 13/2 log t + 1

Q:

In Exercises find the derivative of the function. y = log10 x - 1 X

Q:

Elaborate on the VMFS file system section and discuss data store management. Discuss the challenges presented by the five types of VM migrations.

Q:

On December 31, 2010, Lopez Co (lessee) signed a 3-year, non-cancelable lease for the use of manufacturing equipment now owned by Zinger Inc (lessor). The lease expires December 31, 2013 and has the...

Q:

EXERCISE 13-5 Payback Method [L05] The management of Unter Corporation, an architectural design firm, is considering an investment with the following cash flows: Year Investment Cash Inflow 1 ....