Open the “Secant” interactive figure, which is available in the Video & Resource Library of MyLab Math (under Interactive Figures) or at bit.ly/3raFUGB.
(a) The polynomial function shown in blue has a local maximum of 3 at x = −1. Move Point B to (−1, 3). Move Point A so that the x-coordinate of Point A is less than x = −1. That is, move Point A to the left of Point B. What is the sign of the slope of the secant line for any value of x < −1?
I. Positive

II. Negative
III. Zero

IV. Cannot be determined
(b) Is the polynomial function shown in blue increasing or decreasing on the interval (−∞, −1]?
(c) If a function is increasing on the interval (−∞, −1], then for any x < −1, the slope of the secant line,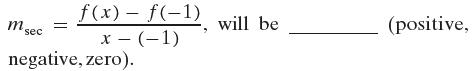

(d) Leave Point B at (−1, 3). Move Point A so that the x-coordinate is near x = 1 (but less than x = 1). That is, move Point A to the right of Point B. What is the sign of the slope of the secant line?
I. Positive

II. Negative
III. Zero

IV. Cannot be determined
(e) Is the polynomial function shown in blue increasing or decreasing on the interval [−1, 1]?
(f) If a function is decreasing on the interval [−1, 1], then for any −1 < x ≤ 1, the slope of the secant line,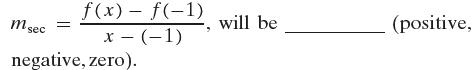

(g) Leave Point B at (−1, 3). Now move Point A toward (−1, 3). What value does the slope of the secant line approach?

f(x)-f(-1), will be x - (-1) m sec negative, zero). (positive,