Show that if a function is defined on an interval symmetric about the origin (so that is defined at x whenever it is defined at x), then Then show that ((x) ( x)) 2 is even and that ((x) ( x)) 2 is odd f(x) f(x) f( x) 2 f(x) f( x) 2 (1)

Question: Show that if a function is defined on an interval symmetric about the origin (so that is defined at -x whenever it is

Show that if a function ƒ is defined on an interval symmetric about the origin (so that ƒ is defined at -x whenever it is defined at x), then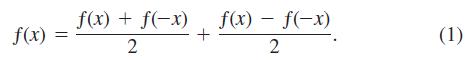 f(x) = f(x) + f(-x) 2 + f(x) = f(-x) 2 (1)

Then show that (ƒ(x) + ƒ(-x))/2 is even and that (ƒ(x) - ƒ(-x))/2 is odd.

f(x) = f(x) + f(-x) 2 + f(x) = f(-x) 2 (1)

Step by Step Solution

★★★★★

3.45 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

First lets simplify the equation fx fx fx2 fx fx2 Combining like terms we get fx ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

The choice between establishing a charitable remainder trust and a charitable lead trust is sometimes influenced by the current interest rates. Explain the possible consequences if a) current...

Show that if A is an infinite set, then whenever B is a set, A B is also an infinite set.

The germination time for a newly developed seed has a normal distribution, with a mean germination time of 16.4 days and a standard deviation of 2.2 days. a. What percentage of the seeds has a...

Chrome File Edit History Bookmarks Profiles Tab Window zoom Q . Tue Nov 14 7:17 PM Harmony G X o Watch Life X U integralsint X A Wilfred DIA X U User repor X U 1300F23W X C Solved We X My Drive - X =...

Let f(x)/[1 F(x)] be the mortality of a subject at time x given that it has survived to this time. A c.d.f. F is said to be smaller than G in the hazard ordering if g(x) 1 G(x) f(x) 1 F(x) for...

Let f (x)/[1 F(x)] be the mortality of a subject at time x given that it has survived to this time. A c.d.f. F is said to be smaller than G in the hazard ordering if g(x) 1 G(x) f (x) 1 F(x) for...

College Algebra MATH 107 Summer, 2017, V1.8 MATH 107 FINAL EXAMINATION This is an open-book exam. You may refer to your text and other course materials as you work on the exam, and you may use a...

I need help College Algebra MATH 107 Fall, 2019, V1.17 MATH 107 FINAL EXAMINATION This is an open-book exam. You may refer to your text and other course materials as you work on the exam, and you may...

Math 107 Final Examination Fall, 2017 1 Math 107 College Algebra Name______________________________ Final Examination: Fall, 2017 Instructor __________________________ Answer Sheet Instructions: This...

Need help on Algebra..any help is appreciated. Answer key is attached There are 30 problems. Problems #112 are Multiple Choice. Problems #13~2l are Short Answer. (Work not required to be shown)...

To what amount will the following investments? accumulate? a. $4,900 invested for 8 years at 11 percent compounded annually. b. $7,900 invested for 6 years at 9 percent compounded annually. c. $7,80...

On 1 January 2017, Magnum acquired 90% of the equity share capital of Picaccio in a share exchange in which Magnum issued two (2) new shares for every three (3) shares it acquired in Picaccio....

A security manager is planning for the needs of an immediate frantic and pressing emergency. Which plan should the security manager focus on developing? Select one: DRP BCP MSA PLA

=+d. The z and t histograms are based on only 200 samples, and they only approximate the corresponding sampling distributions. The 5th percentile for the standard normal distribution is 21.645 and...

Solve each linear programming problem. Maximize z = 3x + 5y subject to x 0, y 0, x + y 2, 2x + 3y 12, 3x + 2y 12

Solve each linear programming problem. Maximize z = 5x + 3y subject to x 0, y 0, x + y 2, x + y 8, 2x + y 10

Solve each linear programming problem. Minimize z = 5x + 4y subject to x 0, y 0, x + y 2, 2x + 3y 12, 3x + y 12

Question 3 Prost plc produces small carbon fibre shells that are one minor component used in the manufacture of racing cars. The manufacture of such shells is a relatively stable process which does...

Inacio Corporation uses the weighted average method in its process costing system Data concerning the first processing department for the most recent month are listed below: 1,800 $ 13,900 $ 6,000 75...

Common stock value Variable growth Lawrence Industries' most recent annual dividend was $1.81 per share (D0=$1.81), and the firm's required return is 14%. Find the market value of Lawrence's shares...