Show that the vertical distance between the line y (b a)x and the upper half of the right hand branch y (b a)x 2 a 2 of the hyperbola (x 2 a 2 ) (y 2 b 2 ) 1 approaches 0 by showing that Similar results hold for the remaining portions of the hyperbola and the lines y (b a)x lim b (2x x a) lim (x b ax lim (x x a) 0

Question: Show that the vertical distance between the line y = (b/a)x and the upper half of the right-hand branch y = (b/a)x 2 - a

Show that the vertical distance between the line y = (b/a)x and the upper half of the right-hand branch y = (b/a)√x² - a² of the hyperbola (x²/a²) - (y²/b²) = 1 approaches 0 by showing that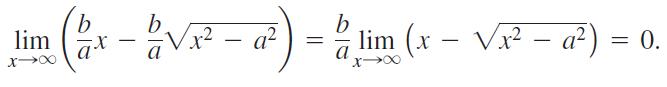 lim b (2x - x - a) - lim (x - b

Similar results hold for the remaining portions of the hyperbola and the lines y = ±(b/a)x.

lim b (2x - x - a) - lim (x - b = ax lim (x - x a) = 0. -

Step by Step Solution

★★★★★

3.38 Rating (170 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To show that the vertical distance between the line y bax and the upper half of the righthand branch ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Show that the vertical distance between a hyperbola x 2 /a 2 - y 2 /b 2 = 1 and its asymptote y = bx/a approaches zero as x, where 0

A 75-kg diver is standing at the end of a diving board while it is vibrating up and down in simple harmonic motion, as indicated in the figure. The diving board has an effective spring constant of k...

For the system shown in Fig. 11.18, calculate the vertical distance between the surfaces of the two reservoirs when water at 10°C flows from A to B at the rate of 0.03 m 3 /s. The elbows are...

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

Possible Multiple Choice Questions for the Exam. Focus on the topics discussed in class. Chapter 1 Multiple Choice Identify the choice that best completes the statement or answers the question. ____...

270 Chapter 4 Applications of Derivatives c. What is the largest area the rectangle can have, and what are its dimensions? 12. Find the volume of the largest right circular cone that can be in- X...

Ap calculus question 268 CHAPTER 3 Applications of Differentiation 66. Consider the situation in Exercise 51 if the cost of laying pipe under the river is considerably higher than the cost of laying...

please help me. 'v'a rious demographic and cardiovascular risk factors were collected as a part of the Prevention of REnal and Vascular END-stage Disease [PREVENDII study, which took plaoe in the...

Please help me. 'v'a rious demographic and cardiovascular risk factors were collected as a part of the Prevention of REnal and Vascular END-stage Disease [PREVENDII study, which took plaoe in the...

You are a store manager for a large, regional department store chain. Company headquarters has asked you to submit an evaluation of your assistant managers performance. The company is considering...

A competitive firm produces a single output using several inputs. The price of output rises by $4 per unit. The price of one of the inputs increases by $2 and the quantity of this input that the firm...

1.25 The Dean of Students at a university mailed out a survey to 400 students. The sample included 100 students randomly selected from each of the freshman, sophomore, junior, and senior classes on...

A rock specimen from a particular area is randomly selected and weighed two different times. Let W denote the actual weight and X1 and X2 the two measured weights. Then X1 W E1 and X2 W E2, where...

Use a graphing utility to graph the function and find the x values at which f is differentiable. f(x) = x 5

Sketch the graph of a function f such that f > 0 for all x and the rate of change of the function is decreasing.

The relationship between f and g is given. Explain the relationship between f and g. g(x) = 5 f(x)

Won Han Co. has four departments: materials, personnel, manufacturing, and packaging. In a recent month, the four departments incurred three shared indirect expenses. The amounts of these indirect...

If the minimum transfer price of the selling division is less than the maximum transfer price of the buying division, the intermediate product should be transferred internally. Do you agree or...

what are some criteria that systems designers should consider when developing managerial reports for an AIS? How do systems desingerners know what to include on reports?