Question: Suppose that r 1 (t) = 1 (t)i + 2 (t)j + 3 (t)k, r 2 (t) = g 1 (t)i +

Suppose that r₁(t) = ƒ₁(t)i + ƒ₂(t)j + ƒ₃(t)k, r₂(t) = g₁(t)i + g₂(t)j + g₃(t)k, lim_t→t₀r₁(t) = A, and lim_t→t₀ r₂(t) = B. Use the determinant formula for cross products and the Limit Product Rule for scalar functions to show that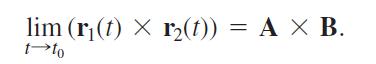 lim (r(t) x r(t)) = A x B. t-to

lim (r(t) x r(t)) = A x B. t-to

Step by Step Solution

★★★★★

3.32 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To begin with lets recall the determinant formula for the cross product of two vectors in terms of t... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

A uniform plane wave of frequency 5 x 10 Hz propagating in a material medium has the following characteristics. (i) The fields are attenuated by the factor e- in a distance of 28.65 m. (ii) The...

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

What is the determinant formula for calculating the cross product of two vectors relative to the Cartesian i, j, k-coordinate system? Use it in an example.

JAVA - RIGHT TO OPEN IMAGE IN A NEW TAB TO VIEW FULL IMAGE. y Help Center? Question 3 What is printed by the function call do Something (3)? public static void do something (int n) { if (n > 0) { do...

2 . What are the values of 1 , ] , and & after the following statements ! ( 15 points ) int i = 2 ; int j = 3 ; int K = 4 ; int x = it j + K ; i = x - i - j ; 1 = j = x - j - K ; i = K = x - I - K; K...

. Question 7 Match each graph with its equation. - v f(x) 1 1 - v f(x) = v f(x) = x a. -5 -4 LAS 4 - v f(x) = 22 - v f(x) = x -v f(x) = Vx -vf(x) = 23 - v f(a) = Vx b. -5 -4 -3 -2 -1. 1 3 4 C.\f\f@...

JAVA - Right click on Image -> Open in image in new tab -> To view clear Image Brightspace Help Center? Question 5 What is the value of k after executing the following code segment? int[] a = new...

The project Director of a PDB project has completed a list of major activities that will be required to install a computer information system in PDB. The list includes estimated completion times for...

8-12 ) REQUIRED RATE OF RETURN Suppose rr = 4%, rM-10%, and bi-1.4. a. What is r, the required rate of return on Stock i? b. Now suppose that rRF (1) increases to 5% or (2) decreases to 3%. The slope...

12/ R REQUIRED RATE OF RETURN Suppose rF-496, M-10%, and bi-1.4 a. What is r, the required rate of return on Stock i? b. Now suppose that rRF (1) increases to 5% or (2) decreases to 3%. The slope of...

You and a friend are thinking about starting a company that would rent residence hall refrigerators at a local college campuses. you will need to do a srategic environmental analysis. Wat would an...

It is essential for managers at any level of organizations to be change leaders in order to sustain change initiatives in their various companies. write about these topics: 1. Discuss and...

The main goals of Canadian tires town strategy are employee learning and retention

=+greater than 0.51 in., the process is shut down for adjustment. The standard deviation for diameter is 0.02 in. What is the probability that the manufacturing line will be shut down unnecessarily?...

Analyze and sketch a graph of the function. Label any intercepts, relative extrema, points of inflection, and asymptotes. Use a graphing utility to verify your results. f(x) = x16 x 2

Considerthefunction f(x) = tan(sin x). (a) Use a graphing utility to graph the function. (b) Identify any symmetry of the graph. (c) Is the function periodic? If so, what is the period? (d)...

The graph of the first derivative of a function f on the interval [4, 2] is shown. Use the graph to answer each question. (a) On what interval(s) is f increasing? (b) On what interval(s) is the graph...

The main regulators of savings institutions today are: Multiple Choice Office of Thrift Supervision (OTS), FDIC, state regulators Office of the Comptroller of the Currency (OCC), FDIC, state...

Mwanza and Tasila are in Partnership. They share profits in the ratio: Mwanza 70 percent Tasila 30 per cent. The following trail balance was extracted as at 31 December 2010 D- G ZMK Office equipment...

Production workers for Fanning Manufacturing Company provided 450 hours of labor in January and 660 hours in February. Fanning expects to use 4,000 hours of labor during the year. The rental fee for...