Question: Suppose (x, y) is continuous over a region R in the plane and that the area A(R) of the region is defined. If there are

Suppose ƒ(x, y) is continuous over a region R in the plane and that the area A(R) of the region is defined. If there are constants m and M such that m ≤ ƒ(x, y) ≤ M for all (x, y)ε R, prove that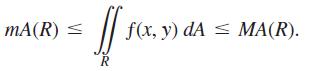 mA(R) < ffs f(x, y) dAMA(R). R

mA(R) < ffs f(x, y) dAMA(R). R

Step by Step Solution

★★★★★

3.40 Rating (156 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Since x y is continuous over R by the Extreme Value Theorem it must attain a minimum value m an... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

The random vector (X, Y) is said to be uniformly distributed over a region R in the plane if, for some constant c, its joint density is (a) Show that 1/c = area of region R. Suppose that (X, Y) is...

Suppose (x, y) is continuous and nonnegative over a region R in the plane with a defined area A(R). If R (x, y) dA = 0, prove that (x, y) = 0 at every point (x, y) R.

A wealthy taxpayer is planning to start an Internet-based business. The taxpayer expects to generate tax losses for at least the first 5 years of the business. The taxpayer also hopes to cash out of...

806 Chapter Fifteen OPTIMIZATION: LOCAL AND GLOBAL EXTREMA If f is not continuous or the region R is not closed and bounded, there is no guarantee that f achieves a global maximum or global minimum...

Calculus 3 Sections 15.1 - 15.2 Reading Assignment: Double Integrals Question 2: Explain each step of the procedure for finding the limits of integration when integrating in the order dx dy. Hint 1:...

1. [-/1 Points] DETAILS LARCALC11 14.5.017. 1. [-/1 Points] DETAILS LARCALC11 14.5.003. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Find the area of the...

1. Let S be the solid of revolution obtained by rotation around the line x=3 of the region R of the plane xy delimited by the curves x=4 , x=5 , y=5/x and y=1/x . We want to calculate the volume of S...

3-4-2 If writing process is bothering you, it's ok to write only correct answer in each question. 1. Let f (x) = v2 - C. Find the average value of f (x) on the interval [-2, 2]. Preview will appear...

10. (a) Consider the triangular region R in the plane with boundary curve C as shown below: 4. 2) C R Let F(r.y) - yi+ (a + 2)rj be a vector field in the plane. R'. Use Green's theorem in the plane...

11. (a) Consider the rectangular region R in the plane with boundary curve C as shown below: y C 2 R 4 Let F(x, y) = (3 + 5)yi + xj be a vector field in the plane, R2. Use Green's theorem in the...

A container is filled with gas at a pressure of 4.0 105 Pa. The container is a cube, 0.10 m on a side, with one side facing south. What is the magnitude and direction of the force on the south side...

Write in the Scheme programming language A binary search tree is a binary tree for which the value in each node is greater than or equal to all values in its left subtree, and less than all values...

301.460 934.601 Deathly Hallows Part I

use a multiple comparison procedure to identify differences in population or treatment means.

In Exercises 4148, find the curvature and radius of curvature of the plane curve at the given value of x. y = 6x, x = 3

In Exercises 53 and 54, find the tangential and normal components of acceleration at the given time t for the space curve r(t). ) = i 6tj + fk, t = 2 3 r(t)

In Exercises 3540, find the tangential and normal components of acceleration at the given time t for the space curve (r)t. r(t) = e t i + 2tj + e -t k, t = 0

Venus Wholesale Co. started carrying a new product in December. Purchases and sales of this product during the month were: Dec. 20 Purchased 110 units at $81 per unit. Dec. 26 Sold 100 units. Dec. 28...

PLEASE JUST DO PROBLEM 4, no need to do the rest, thank you. The problem needs equations from other problems too. Please show all the work when solving problem 4, thanks :) Suppose that the OLS...

Premium on Bonds Payable a. is deducted from bonds payable on the balance sheet. b. has a debit balance. c. is a contra account. d. is considered to be a reduction in the cost of borrowing