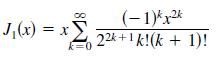
The Bessel function of order 1 is (a) Show that the series converges for all x (b) Show that the series is a solution of the differential equation (c) Use a graphing utility to graph the polynomial composed of the first four terms of J 1 (d) Use J 0 from Exercise 65 to show that J 0 '(x) J 1 (x) Use J 0 from Exercise 65 The Bessel function of order 0 is ( 1) xk J(x) x 22k k (k 1) k 0

Question: The Bessel function of order 1 is (a) Show that the series converges for all x. (b) Show that the series is a solution of

The Bessel function of order 1 is

(-1)*.xk J(x) = x 22k+k!(k + 1)! k=0

(a) Show that the series converges for all x.

(b) Show that the series is a solution of the differential equation

(d) Use J₀ from Exercise 65 to show that J₀'(x) = -J₁(x).

Use J₀ from Exercise 65

The Bessel function of order 0 is

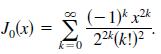
(-1)*.xk J(x) = x 22k+k!(k + 1)! k=0

Step by Step Solution

★★★★★

3.44 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

answer a To show that the series converges for all x we can use the ratio test The ratio test states that if the limit of the absolute value of the ra... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

In Example 6 we considered a bacteria population that doubles every hour. Suppose that another population of bacteria triples every hour and starts with 400 bacteria. Find an expression for the...

The Bessel function of order 0 is (a) Show that the series converges for all x. (b) Show that the series is a solution of the differential equation (c) Use a graphing utility to graph the polynomial...

The function J1 defined by Is called the Bessel function of order 1. (a) Find its domain. (b) Graph the first several partial sums on a common screen. (c) If your CAS has built-in Bessel functions,...

bessels functionare important in applications to Bessel functions are important in applications to wave propagation and static potentials (google it!). The Bessel function of order 1 is given by What...

3. The growth of bacteria (N cells) in a chemostat can be modeled as: dN = kN dt C. where k = 3 h is a first order rate constant. a. Show that N(t) = N, ekt is the solution to this differential...

Python - Applied Math - Radial Basis Function Collocation Method Bessel's Functions are special functions that play an important role in the modeling of physical phenomena. The particular one we will...

Specially pls 1. Recall the Bessel function of order 0, Jo(x) from lectures: (-1)~ x2n Jo(a) = 22n (n!) 2 (1) n=0 We learned that the Bessel function appears in many applications in science and engi-...

I. Foundations/Comprehension (No technology allowed, show all work!) 1. Solve the following differential equations, using the method of separation of variables (4 points each): a) y' = 1-xty-xy...

please help with code. In either c++, python, or matlab @ how to screenshot on pc. Goog | Project1_135B(1).pdf C Get Homework Help With Chege. Bb a https://ilearn.ucr.e...

8. Let n ~ 0 be a fixed nonnegative integer and recall that O! := 1. The Bessel function of order n is the function defined by 00 (-l)k (x)n+2k Bn(x) := {; (k!)(n + k)!"2 . (a) show that Bn (x)...

How are secondary markets organized? MINI CASE Assume that you recently graduated with a degree in finance and have just reported to work as an investment advisor at the brokerage firm of Balik and...

Save-the-Earth Co. reports the following income statement accounts for the year ended December 31. Sales discounts Office salaries expense Rent expense-Office space Advertising expense Sales returns...

Allows you to change the processor mode from a programmer / operator interface device, allows you to perform online program editing. RUN ROM REM RAM

4. Use the simulation results to estimate the desired probabilities. a. Estimate the probability that more than five pairs must be treated before a conclusion can be reached. (Hint: P(more than 5) 5...

Using vectors, prove the Law of Sines: If a, b and c are the three sides of the triangle shown in the figure, then sin A ||al| sin B ||b|| sin C ||c|| A B b a C

Find the component form of given its magnitude and the angle it makes with the positive x-axis. ||v|| = 8,0 = 60

Let u = PQ and v = PR (a) Write u and v in component form (b) Write u and v as the linear combination of the standard unit vectors i and j (c) Find the magnitudes of u and v (d) Find 2u + v P =...

The accounting principle that guides accountants, when faced with a recognition dilemma, to choose the alternative that produces the lowest net income is referred to as: the matching concept....

heridan AME ENGAGE English (en) rrect out of Take me to the text Feng Inc. is planning to purchase $346,000 worth of 6-year bonds issued by George Company, a publicly traded company on January 1,...

what would be the correct jounral entry The company received a notice from the bank related to a $100 NSF check deposited. Donald and Joe think the customer is good for this amount, and they believe...