The figure shows the graphs of the function f(x) = sin(x/4) and the second-degree Taylor polynomial P 2 (x) = 1 - ( 2 /32)(x

The figure shows the graphs of the function f(x) = sin(πx/4) and the second-degree Taylor polynomial P₂(x) = 1 - (π²/32)(x - 2)² centered at x = 2.

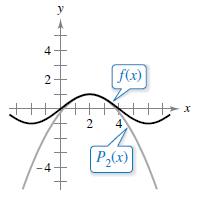
(a) Use the symmetry of the graph of f to write the second degree Taylor polynomial Q₂(x) for f centered at x = -2.

(b) Use a horizontal translation of the result in part (a) to find the second-degree Taylor polynomial R₂(x) for f centered at x = 6.

(c) Is it possible to use a horizontal translation of the result in part (a) to write a second-degree Taylor polynomial for f centered at x = 4? Explain.

4 2 -4 y f(x) 2 4 P(x)