The Mean Value Theorem for double integrals says that if f is a continuous function on a plane region D that is of type I or II, then there exists a point (x₀, y₀) in D such that

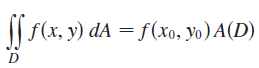
Use the Extreme Value Theorem (14.7.8) and Property 15.2.11 of integrals to prove this theorem. (Use the proof of the single-variable version in Section 6.5 as a guide.)

Transcribed Image Text:

| f(x, y) dA = f(xo, Yo) A(D)