The problem of locating a planet in its orbit at a given time and date eventually leads to solving “Kepler” equations of the form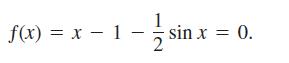

a. Show that this particular equation has a solution between x = 0 and x = 2.

b. With your computer or calculator in radian mode, use Newton’s method to find the solution to as many places as you can.

f(x) = x - 1 - -1/2 sin x = 0.