Question: The series converges to sin x for all x. a. Find the first six terms of a series for cos x. For what values of

The series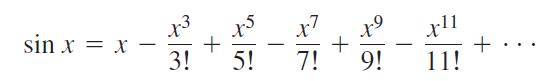 sin x = x - + + 11! +

converges to sin x for all x.

a. Find the first six terms of a series for cos x. For what values of x should the series converge?

b. By replacing x by 2x in the series for sin x, find a series that converges to sin 2x for all x.

c. Using the result in part (a) and series multiplication, calculate the first six terms of a series for 2 sin x cos x. Compare your answer with the answer in part (b).

sin x = x - + + 11! +

Step by Step Solution

★★★★★

3.39 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a The series for cos x is given by cos x 1 x22 x44 x66 To find the first six terms we substitute x 0 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

The solution containing no added KNO3 for Figure 7-1 contains 5.0 mM Fe(NO3)3, 5.0 M NaSCN, and 15 mM HNO3. We will use Davies activity coefficients to find the concentrations of all species in the...

Construct a confidence interval for p, - p, at the given level of confidence. X, = 364, n, = 539, x, = 404, n, = 556, 90% confidence %3D %3D The 90% confidence interval for p, - p2 is ( ). (Use...

In Exercises 1-2: (a) Find the coordinate vectors [x]B and [x]C of x with respect to the bases B and C, respectively. (b) Find the change-of-basis matrix PCB from B to C. (c) Use your answer to part...

51. The series x3 x5 x7 x9 x11 smx=x++ll! converges to sin x for all x. +... 3. Find the first six terms of a series for cos x. For What values of x should the series converge? b. By replacing x by...

K xn Consider the series E n=2 n( Inn) (a) Find the series' radius and interval of convergence. (b) For what values of x does the series converge absolutely? (c) For what values of x does the series...

00 onsider the series E (-1)"(6x + 7)" n=0 ) Find the series' radius and interval of convergence. For what values of x does the series converge absolutely? For what values of x does the series...

3. W 1 3n Considsrthe series 2 [1 + F] x5\". n = 1 {a} Find the series' radius and interval of convergence. [It] For what values of I does the series converge absolutely? [ct For what values ofx does...

Ch7 Sequences Quiz Pre-Calculus OL v3 B - Cohen, Dana / Module 7: Sequences, Series and Proof by Induction J L 4. Find a recursive rule for the nth term of the sequence. -7, 0, 7, 14, ... an= an-1 -...

handwrit.e and show all work and steps 5. Find the limit of the function algebraically. (2 points) x2 + 3 lim X-+0 * 46. A building has an entry the shape of a parabolic arch 22 ft high and 28 ft...

1 8. Verify that Ento 2i n function illustrated in Figure 6, defined by f(0) = 0, and etx f(x) = is the Fourier series of the 2-periodic sawtooth 2 2 KIN - 0 x 2 x 2 Note that this function is not...

The deregulation of financial markets has enabled Australian banks to look at international financial markets as an alternative cost efficient source of funds. Students will research the...

Montross Seating manufactures desk chairs for commercial distribution. Each chair is produced at a cost of $15 and sold for $25. What is the contribution margin ratio for desk chairs?

3-11 Give some examples of activities, other than manufacturing, which require the planning of future operations.

_________A relatively permanent committee charged with performing some recurring task is called a. an ad hoc committee. b. a standing committee. c. a task force. d. a managerial committee. e. a...

Find equations of the osculating circles of the ellipse 9x 2 + 4y 2 = 36 at the points (2, 0) and (0, 3). Use a graphing calculator or computer to graph the ellipse and both osculating circles on the...

Find equations of the osculating circles of the parabola y = 1/2 x 2 at the points (0, 0) and (1, 1/2). Graph both osculating circles and the parabola on the same screen.

At what point on the curve x = t 3 , y = 3t, z = t 4 is the normal plane parallel to the plane 6x + 6y - 8z = 1?

1. Aadakilerden hangisi kurumsal i biiminin gl ynlerinden biridir? A. letmenin snrl mr B. Sermayeye snrsz eriim C. Snrsz sorumluluk D. Gelirin ifte vergilendirilmesi 2. Bir finansal arac, aadaki...

elizabeth soltis owns and operates aunt ibby's styling salon. a year-end work sheet is provided on the next page. using this information, prepare adjusting entries, financial statements, and closing...

Sweeten Company had no jobs in progress at the beginning of the year and no beginning inventories. It started, completed, and sold only two jobs during the yearJob P and Job Q. The company uses a...