Use a CAS to perform the following steps for the given graph of the function over the closed interval.

a. Plot the curve together with the polygonal path approximations for n = 2, 4, 8 partition points over the interval. (See Figure 6.22.)

b. Find the corresponding approximation to the length of the curve by summing the lengths of the line segments.

c. Evaluate the length of the curve using an integral. Compare your approximations for n = 2, 4, 8 with the actual length given by the integral. How does the actual length compare with the approximations as n increases? Explain your answer.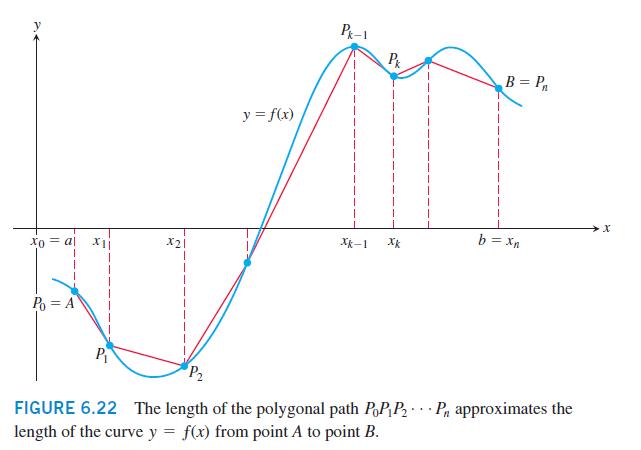

ƒ(x) = x³ - x², -1 ≤ x ≤ 1

Xo = 8 Po = A P X21 y = f(x) Pk-1 Xk-1 B = P b = xn FIGURE 6.22 The length of the polygonal path PoPIP P approximates the length of the curve y = f(x) from point A to point B.