Question: Use substitution (as in Example 4) to find the Taylor series at x = 0 of the functions. EXAMPLE 4 Using known series, find the

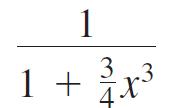
Use substitution (as in Example 4) to find the Taylor series at x = 0 of the functions. EXAMPLE 4 Using known series, find the first few terms of the Taylor series for the given function using power series operations. (b) e

EXAMPLE 4 Using known series, find the first few terms of the Taylor series for the given function using power series operations. (b) e cos x (a) (2x (2x + x cos x) (a) (2x (2x + x cos x) = (b) e cos x = = 2 = 1 + x + 2 1 x + X 3.x 3 3! = ( + x + + 1 x 3 + + 6 4! x5 3.4! x2k (2k)! + (-1). = 1 + x + + + + ) ( - # - # ----) 1 2! 3! 4! 4! + 72 + + - - -) - ( ++ ++) 3! 4! 2!2! 2!3! + +6 214! +

Step by Step Solution

★★★★★

3.45 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The Taylor series expansion of a function fx about x 0 is given by fx f0 f0x f02x2 f03x3 where fx f... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Use substitution (as in Example 4) to find the Taylor series at x = 0 of the functions. tan -1 (3x 4 ) EXAMPLE 4 Using known series, find the first few terms of the Taylor series for the given...

Use substitution (as in Example 4) to find the Taylor series at x = 0 of the functions. ln (1 + x 2 ) EXAMPLE 4 Using known series, find the first few terms of the Taylor series for the given...

Use substitution (as in Example 4) to find the Taylor series at x = 0 of the functions. cos (x 2/ 3 /2) EXAMPLE 4 Using known series, find the first few terms of the Taylor series for the given...

Use substitution (as in Example 4) to find the Taylor series at x = 0 of the functions. e -5x EXAMPLE 4 Using known series, find the first few terms of the Taylor series for the given function using...

Use substitution (as in Example 4) to find the Taylor series at x = 0 of the functions. e -x/2 EXAMPLE 4 Using known series, find the first few terms of the Taylor series for the given function using...

Use substitution (as in Example 4) to find the Taylor series at x = 0 of the functions. cos 5x 2 EXAMPLE 4 Using known series, find the first few terms of the Taylor series for the given function...

Use substitution (as in Example 4) to find the Taylor series at x = 0 of the functions. 5sin (-x) EXAMPLE 4 Using known series, find the first few terms of the Taylor series for the given function...

2. [0/1 Points] DETAILS PREVIOUS ANSWERS BERRAPCALC7 7.5.003. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Use Lagrange multipliers to maximize the function f(x, y) subject to the constraint. (The...

LLED has purchased a new chip making machine for $1,500,000 with a salvage value of $100,000 in 10 years. The LLED company is trying to determine the best method of depreciation. Create a table and...

Determine the electric field due to the following potentials: (a) V= x2 + 2y2 + 4z2 (b) V = sin(x2 + y2 + z2)1/2 (c) V = 2(z + l)sin (d) V = er sin cos 2

2. Apa manfaat, biaya, dan risiko dari strategi pendanaan yang agresif dan strategi pendanaan yang konservatif? Di bawah strategi manakah pinjaman yang diambil sering melebihi kebutuhan dana yang...

Let X,,..., X., be a random sample from a gamma distribu- tion with parameters a and B. a. Derive the equations whose solutions yield the maximum likelihood estimators of a and B. Do you think they...

Sketch the region of integration and change the order of integration. T/2 f(x, y) dy dx cos x

Sketch the region of integration and change the order of integration. V4-y2 f(x, y) dx dy |-2 Jo

Sketch the region of integration and change the order of integration. 2 (In x f(x, y) dy dx 1

Music Now plans to sell 6,000 MP3 players at $60 each in the coming year. Variable cost per unit is $12 and total fixed cost is $24,000 A. Calculate the variable cost ratio B. calculate the...

Zola Company manufactures and sells one product. The following information pertains to the companys first year of operations: Variable cost per unit: Direct materials $ 13 Fixed costs per year:...

All of the following statements about intangible benefits in capital budgeting are correct, except that they __________. include increased quality and employee loyalty. are difficult to quantify are...