Use the following steps to prove that the binomial series in Equation (1) converges to (1 + x)^m.

a. Differentiate the series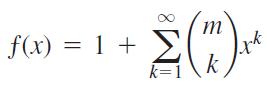

to show that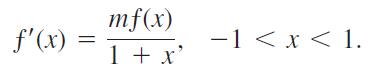

b. Define g(x) = (1 + x)^-m ƒ(x) and show that g′(x) = 0.

c. From part (b), show that ƒ(x) = (1 + x)^m.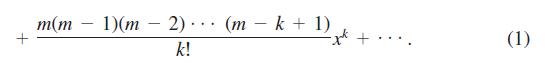

f(x) = 1 + m (1).** k=1